La aerodinámica ha sido, sin duda, uno de los principales intereses de la Torre Eiffel. Con la radiodifusión es el área donde se ha realizado el mayor progreso. La instalación de un laboratorio en el segundo piso permitió el estudio de la resistencia al aire de los materiales, de los cuales deducimos las propiedades mecánicas utilizadas hoy en día en la aeronáutica.
Un número muy pequeño de experimentos se realizaron hasta el siglo XIX sobre la caída de los cuerpos teniendo en cuenta la resistencia que el aire se opone a su movimiento. Sin embargo, aparte del interés científico que presenta, el estudio de esta pregunta permitiría resolver un gran número de dificultades que se encuentran en cada momento en diversas aplicaciones prácticas, la resistencia del aire a los trenes de los ferrocarriles. y barcos en movimiento, dirección de globos, problemas de aviación, influencia del viento en edificios, uso del viento como motor, etc.
Hasta finales del siglo XIX, los experimentos realizados sobre este tema se ejecutaron principalmente imprimiendo a los cuerpos un movimiento de rotación obtenido con la ayuda de una especie de carrusel. Según los propios autores, los métodos empleados dan solo resultados incompletos debido al arrastre del aire, la fuerza centrífuga, etc. Además, la velocidad que se puede lograr es muy limitada. Pensamos que la Torre Eiffel ofrecía condiciones particularmente ventajosas para estudiar más completamente esta interesante pregunta y para abordar directamente el estudio del movimiento rectilíneo.
Principio del metodo
Cuando un cuerpo se mueve en el aire, experimenta una resistencia que aumenta con la velocidad del movimiento. Supongamos que este cuerpo es solicitado por una fuerza constante, como lo es, por ejemplo, por su propio peso, cuando se abandona en caída libre. Si, en lugar de lanzarse al aire, estuviera en un vacío, su velocidad, inicialmente cero, aumentaría constantemente y su movimiento se aceleraría indefinidamente. Si él está en el aire, no será lo mismo. A medida que aumenta la velocidad del móvil, experimentará una resistencia creciente, de modo que su movimiento dejará de acelerarse y se volverá uniforme precisamente cuando la resistencia del aire equilibrará exactamente el efecto de la gravedad en el cuerpo.
Si medimos, por un lado, la velocidad V del cuerpo en el momento en que su movimiento se vuelve uniforme, y por otro lado su peso P, sabremos que la fuerza ejercida por el aire sobre el cuerpo animado del cuerpo. la velocidad V es precisamente P.
Al aumentar el peso del cuerpo, sin modificar su superficie, mediante la adición de un peso adecuado, se aumentará al mismo tiempo la velocidad V del movimiento uniforme del límite, de modo que la comparación de los diversos valores de P con los ladrones correspondientes de V revelará la ley de variación de la resistencia en función de la velocidad.
Para poner en práctica este método, el aparato empleado se basa en el siguiente principio:
Imagine un cable largo y delgado subdividido en secciones iguales, por ejemplo, 20 m. Deje que las subdivisiones de las secciones consecutivas estén ligeramente unidas a los puntos de suspensión, dejando las diferentes secciones sucesivas de 20 m entre ellas. Supongamos que en los puntos de suspensión hay contactos eléctricos capaces de funcionar bajo la influencia de una tracción muy leve del cable y unidos a un lápiz óptico adaptado a un cilindro giratorio de acuerdo con la disposición conocida. Dejemos caer el cuerpo pesado en el extremo libre del cable.
El momento de la salida será registrado en el cilindro por el primer contacto. Tan pronto como el cuerpo, al caer, habrá recorrido 20 m, habrá llevado consigo el primer tramo de alambre que se habrá desarrollado verticalmente siguiendo el cuerpo; El segundo contacto funcionará a su vez, y así sucesivamente. Si se agrega una bifurcación de ajuste al cilindro, por ejemplo, 100 vibraciones por segundo, la gráfica trazada en el cilindro indicará, en centésimas de segundo, después de qué intervalos de tiempo el cuerpo ha viajado 20, 40, 60 m . Tan pronto como el movimiento se vuelva uniforme, veremos en el gráfico que los contactos sucesivos operarán en intervalos de tiempo equidistantes. Estos intervalos, medidos en centésimas de segundo, por las sinuosidades de la curva del diapasón, obtendremos inmediatamente la velocidad uniforme del móvil.
Arreglo práctico del dispositivo
Aquí hay una descripción del dispositivo de caída, descripción hecha por el mismo Gustave Eiffel.
El aparato que llevaba la placa de prueba cayó en caída libre, y fue guiado por un cable vertical de 115 metros de longitud, que dio velocidades de hasta 40 metros por segundo. Consiste esencialmente en una masa pesada que empuja la placa frente a ella, a través de dos resortes calibrados. Su acción es antagónica a la resistencia del aire, por lo que el desplazamiento, en relación con el resto del aparato, de la parte móvil que lleva la superficie permite evaluar la tensión de los resortes, de los cuales se deduce La propia resistencia. Para este propósito, una horquilla de sintonización a 100 vibraciones por segundo, puesta en movimiento al comienzo de la caída y asegurada a la parte móvil, está provista de un estilete que puede moverse a lo largo de un generador de un cilindro vertical transportado por El marco del dispositivo. Este cilindro, cubierto con un papel ennegrecido con humo, gira con una velocidad proporcional a la velocidad de caída, gracias a un rodillo provisto de estrías finas que ruedan a lo largo del cable en el que se presiona energéticamente. Al mismo tiempo, las vibraciones de la horquilla de afinación inscriben en el cilindro el tiempo transcurrido desde el origen de la caída. Como, por otra parte, las abscisas son proporcionales a los espacios atravesados en la caída, el diagrama proporciona, en una misma curva y en cualquier momento de la caída, las tres cantidades que nos interesan: la fuerza, por la medida de las ordenadas. Representando la tensión de los resortes, el espacio atravesado, mediante la lectura de las abscisas y, finalmente, el tiempo, mediante el recuento de las vibraciones, de las que se deduce en cada momento la velocidad y la resistencia.
En la práctica, sería imposible dejar flotando en el espacio las secciones sucesivas del cable, que por el efecto de las corrientes de aire se entrelazan entre sí. Esta desventaja ha sido evitada por el siguiente artificio.
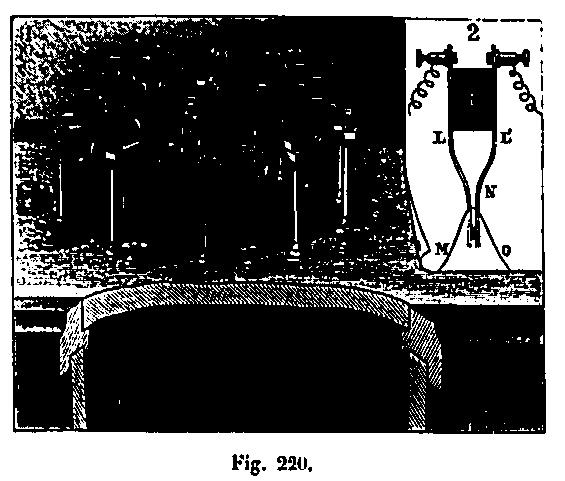
Cada sección del alambre se enrolla en un cono de madera C1, C2, C3 (ver Fig. 220) fijado verticalmente, la punta girada hacia abajo. Es fácil ver que el hilo arrastrado por la caída del móvil lo sigue con la mayor facilidad; Debido a su forma cónica, estas bobinas, aunque inmóviles, permiten que este hilo se despliegue, por así decirlo, sin fricción. También hemos evaluado mediante una medición directa, como se verá más adelante, el retraso que puede surgir de una resistencia para desenrollar el cable.

El laboratorio del 2º piso de la torre Eiffel
Los contactos eléctricos destinados a registrar cada trayecto de 20 m están formados por dos cuchillas metálicas LL 'aisladas en 1 por una pieza de ebonita y cuyos extremos se tocan a través de contactos de platino. Este tipo de pinza es atravesada por una corriente eléctrica que animará la pluma de la grabadora y se interrumpe cuando las dos ramas se separan. Al pasar de un cono C1, C2 al siguiente, se activa en el intervalo libre que deja entre ellos las dos ramas de cada abrazadera, inmediatamente por encima del contacto de platino. Cuando el cono C se desenrolla, el alambre fijado a la parte móvil por un momento extiende las ramas de la pinza y abre la corriente que se restaura inmediatamente. Es entonces cuando la pluma de la grabadora deja una marca en el cilindro giratorio. Luego el cono C2, se despliega sucesivamente; La segunda pinza se abre después de un nuevo recorrido de 20 m, y así sucesivamente. Las cuchillas LL 'que constituyen cada abrazadera son muy flexibles, la resistencia que se oponen a la separación por el paso del cable es extremadamente baja. En las pruebas realizadas para evaluar esta resistencia, un peso de 2 g que caía desde la altura de 10 cm era suficiente para eliminar estas cuchillas. Un cálculo muy simple permite garantizar que este esfuerzo retrasaría en menos de 1 mm la caída de un peso de 1 kg después de un recorrido de 20 m.
Para evaluar la doble resistencia que puede venir del desenrollamiento del cable, su fricción en el aire y otras resistencias pasivas, se han utilizado varios métodos:
1. Una flecha cilíndrica de madera ponderada se ha caído en su parte superior por una masa metálica que termina en un punto cónico. Debido a su pequeña sección y su forma alargada, esta flecha debe experimentar solo una pequeña resistencia del aire. Debe, por lo tanto, tomar un movimiento de caída poco diferente al que tendría en el vacío. Esta última conclusión todavía es aplicable, si las resistencias posibles debidas al cable impulsado son despreciables. Ahora, en varios experimentos muy concordantes, se ha encontrado que la duración total de la caída de esta flecha no difiere de la de la caída teórica en el vacío de más de 20/1000 de su valor.
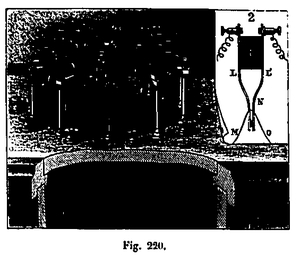
Diagrama del aparato para medir la caída de los cuerpos
2. Un segundo medio de verificación consistió en dejar el móvil completamente libre y no conectado al cable. El momento de su partida es registrado por la pluma eléctrica cuyo circuito se interrumpe por la caída del cuerpo en el momento en que comienza a moverse. Al llegar al suelo, este móvil golpeó un panel de madera sostenido por resortes y a través de una corriente que anima la pluma de la grabadora. En el momento del choque, el panel cede y se interrumpe la corriente, de modo que se registra el momento preciso de la llegada y el de la salida. Al comparar el tiempo total de caída libre así obtenido con el dado por el mismo móvil conectado al cable y hacer que las pinzas funcionen, la diferencia en estas duraciones representa la suma de los retrasos experimentados por este móvil desde las resistencias pasivas debidas a la dispositivo. En dos experimentos consecutivos realizados con un cilindro de cobre que pesa 2080 g, se ha encontrado que la diferencia en los tiempos de caída de este cilindro, cuando está unido al cable y cuando está completamente libre, es 0, 04 segundos una duración total de caída de 5 segundos. La demora debida a la conducción del cable es, por lo tanto, inferior al 1%.
El aparato hizo posible verificar que la resistencia opuesta por el aire a los planos de igual superficie, moviéndose en una dirección normal a estos planos, es independiente de su forma. Para superficies circulares, cuadradas y triangulares, se han encontrado tiempos de caída iguales, como se puede ver en la Figura 321, líneas 3 y 4. Esta figura es la reducción de un cuarto de punto de los gráficos reales. La curva de la bifurcación de sintonización se traza suponiendo que realiza 25 vibraciones por segundo.
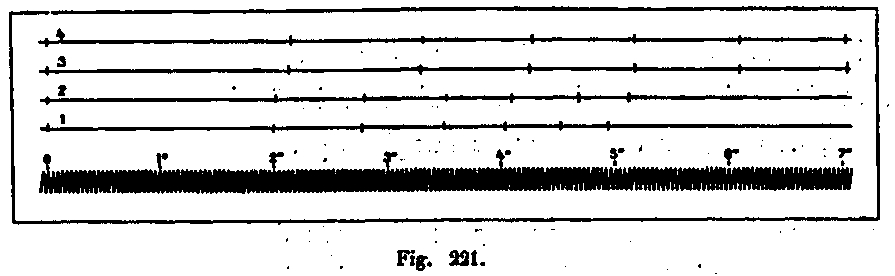
También se ha verificado que la resistencia experimentada por un avión que opera en el aire es proporcional a su superficie. Dos planos cuadrados cuyas superficies estaban entre ellos como 1 y 2 se ponderaron con pesos que estaban en la misma proporción. La duración de la caída fue de 6,92 segundos y 6,96 segundos, respectivamente, aproximadamente el mismo número y según el cual se debe aceptar la proporcionalidad.
Los experimentos más numerosos se han centrado en la evaluación en kilogramos, por metro cuadrado, de la resistencia opuesta por el aire a una superficie plana móvil y en la búsqueda de la ley de variación de esta resistencia en función de la velocidad. Hemos visto anteriormente cómo podemos obtener esta ley al evaluar el peso del móvil y al medir su velocidad cuando el movimiento de caída se ha uniformado. En todos los experimentos en cuestión, el peso de las superficies empleadas se ajustó para obtener la uniformidad del movimiento después de un curso de entre 60 y 100 m.
Sabemos que generalmente se acepta que la resistencia del aire es proporcional a la superficie y al cuadrado de la velocidad del cuerpo en movimiento, al menos para velocidades moderadas como las que se mencionan aquí. La fórmula que expresa esta ley es: P = R S V2.
P es la presión del aire en el cuerpo, S su superficie y V su velocidad. Los ingenieros generalmente adoptan un valor de R = 0.12248, donde P se expresa en kilogramos por metro cuadrado, S en metros cuadrados y V en metros por segundo. Si esta fórmula es correcta, el valor de R calculado de acuerdo con ella, utilizando una serie de valores correspondientes de P y V, para planos de la misma superficie S, debe ser siempre el mismo para las velocidades diferente. Los experimentos llevados a cabo en la Torre Eiffel han dado para los valores de R, por lo que los números calculados se acercan entre sí, por lo que es necesario admitir la precisión de la fórmula desde el punto de vista práctico para velocidades de hasta a 25 m por segundo
Pero el valor numérico de R así obtenido es muy diferente del adoptado hasta ahora. Los diversos valores encontrados para R oscilan entre 0.069 y 0.071. El valor medio a admitir es, por tanto, de 0.070.
La determinación de este coeficiente, cuyo valor 0.07 es muy diferente del número 0.125 admitido por las fórmulas estándar y que reduce la presión del viento a 57% de la que generalmente se adoptó, también fue objeto de investigación por parte de El Sr. Langley (Experimentos en aerodinámica) e informó en las Actas de la Sociedad de Física (marzo de 1892). Estos experimentos se realizaron utilizando un carrusel de 9 m de radio, al final del cual se fijó un móvil móvil en todas las direcciones alrededor de su centro, mediante una suspensión de cardán y para medir su tamaño. y en la dirección de presión que actúa sobre un plano. Este plano en sí mismo, en el sentido de su longitud, podría colocarse en una dirección paralela u oblicua a la dirección del movimiento. Para una planta cuadrada de 505 mm de lado y velocidades que varían entre 5 my 11 m, se verificó la fórmula general anterior. Esta fórmula es para planos normales muy poco diferente de la encontrada por MM. Cailletet y Colardeau, lo que da unos resultados un poco más fuertes.
Evolución del dispositivo

Túnel de viento de Gustave Eiffel
Desafortunadamente, este laboratorio no fue lo suficientemente eficiente, y las técnicas que lo mejoraron diseñaron un soplador para probar los materiales en condiciones más cercanas a la realidad. Este túnel de viento le permitió mejorar su conocimiento de las propiedades de los materiales frente al viento. Realizó más de 5,000 pruebas en la resistencia del aire de las alas y las hélices, lo que permitió a los ingenieros de aviación diseñar los perfiles de las alas de los aviones que se construirán en los años posteriores a la construcción de la torre. El túnel de viento estuvo en funcionamiento desde agosto de 1909 hasta diciembre de 1911. A partir de 1912 se trasladó a Auteuil, rue Boileau, el municipio de París, considerando el edificio feo. Este nuevo laboratorio estaba equipado con dos turbinas (1 y 2 metros). El de 1 m fue desmantelado en 1933, pero el otro ... ¡sigue en funcionamiento!
Conclusión
Con respecto a la caída de los cuerpos y la resistencia del aire, la Torre Eiffel ha sido de gran utilidad. Fue desde el laboratorio que Eiffel instaló en el segundo piso que el Sr. Louis Callet, miembro del Instituto, y el Sr. R. Colbert, hicieron algunos experimentos interesantes cuyos informes se entregaron en "Les Actas de la Academia de Ciencias "(1892) y" Nature "(9 de julio de 1892), luego en" Los Informes de la Sociedad de Física "del 4 de noviembre de 1892. En el siguiente enlace tiene la cuenta Reporte completo de estas experiencias tal como fue escrito en el momento.