Cálculo de fuerzas debidas al viento

Principio de construcción

Supongamos por un momento que hemos dispuesto en las caras una celosía simple que forma una pared resistente a las fuerzas de cizallamiento del viento, cuyos componentes son P ', P ", P' '', P" "(Fig. 8). Se sabe que para calcular las fuerzas que actúan en tres piezas cortadas por un plano NM, es suficiente determinar la P resultante de todas las fuerzas externas que actúan sobre la sección y descomponer esta resultante en tres fuerzas que pasan a través de las tres barras cortadas.

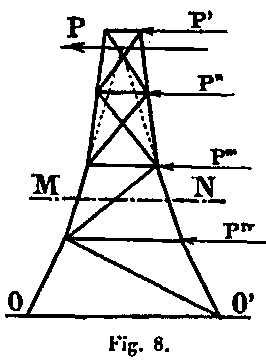
Si la forma del sistema es tal que para cada sección horizontal MN, las dos vigas extendidas tienen su intersección en la dirección de la fuerza externa P, el esfuerzo en la barra de celosía será cero y podemos eliminar esta barra. Es la aplicación de este principio lo que constituye una de las peculiaridades del sistema empleado para la construcción de la Torre, al menos en su mitad inferior, y lo que determina su forma externa. Permite, al eliminar todos los enrejados en la mayor parte de su altura, constituirlos mediante cuatro montantes aislados, simplemente conectados en el nivel de la 1ª y 2ª etapa mediante cinturones horizontales. De este modo, se dirige a uno a doblar la dirección de cada uno de los elementos de los montantes en una curva que debe confundirse con la curva de presión, si se propone tener fuerzas de corte nulas; pero esto solo es factible para una sola hipótesis.

Dado que proponemos examinar varias hipótesis sobre la distribución del viento, tendremos que dibujar una fibra media que se aproxime al promedio de las curvas de presión, a fin de minimizar los momentos de flexión que pueden ocurrir según una o la otra hipótesis. Observemos que la curva de las presiones correspondientes a un viento de intensidad constante en toda la altura de la Torre es independiente del valor absoluto de esta intensidad y, por consiguiente, esta intensidad no tiene influencia en la forma misma de la tour. Dado que las curvas de presión no pasan exactamente en el centro de los montantes, es decir, no se combinan completamente con el resultado promedio de la fibra, los momentos de flexión y las fuerzas de corte que deben calcularse.

Intensidad del viento

Hemos admitido varias hipótesis:

a. El primero da lugar, en general, a la fatiga máxima: es la de un viento de 300 kg por metro cuadrado que actúa uniformemente sobre toda la altura de la torre. De acuerdo con la fórmula generalmente aceptada, P = 0.12V2, donde P es la presión por metro cuadrado y V es la velocidad, esta presión de 300 Kg corresponde a una velocidad de 50 metros por segundo, que es la de un gran huracán. . Cualquiera que sea la incertidumbre en la medición de tales velocidades, puede ser cierto que nunca se ha observado tal situación en nuestras regiones, al menos cerca del suelo; Si se realizaran, darían lugar a desastres reales. Una presión de 150 Kg vuelca los trenes, como se observó en Rivesaltes, y la de 270 Kg es el máximo permitido por la Circular Ministerial del 29 de agosto de 1891 para el cálculo de las obras de arte. Esta última figura es la que generalmente se adopta en estos cálculos.

Sin embargo, debemos decir que las ráfagas de 40 metros de velocidad ya han sido indicadas por los instrumentos colocados en la parte superior de la Torre, todas las reservas hechas sobre la exactitud de estas indicaciones. Corresponden, según la fórmula, a presiones de 200 kg por metro cuadrado. Pero, como se dirá más adelante, tenemos razones para pensar, a partir de experimentos de presión directa, que la fórmula anterior da resultados demasiado altos y que el coeficiente de 0.12 debe reducirse a 0.09, que en realidad daría vientos de 50 metros, 225 Kg de presión por metro cuadrado y para vientos de 40 metros, 150 Kg de presión. Nuestra suposición de 300 Kg correspondería a un viento de 60 metros por segundo o 216 kilómetros por hora, lo que nunca se observó. Suponiendo que suceda en un cierto punto en la parte superior, disminuirá rápidamente a medida que se acerca al suelo.

b. Esta consideración nos ha llevado a examinar una segunda hipótesis que también es excesiva, aunque más cercana a la realidad: es la de un viento que alcanza los 400 kg en la cima y disminuye gradualmente a 200 kg en la superficie del suelo. En cualquier punto, ubicado a una altura h sobre el suelo, la intensidad del viento será de 200 Kg + - x h.

Con el coeficiente de 0.12, las velocidades correspondientes son 58 metros en la parte superior y 40 metros en la base; con el coeficiente de 0.09, las velocidades serían de 66 metros y 47 metros. Estas dos hipótesis conducen a los límites extremos de los coeficientes de trabajo y son lo que usamos para determinar las secciones de los diversos elementos de la Torre. Sin embargo, una vez que las secciones determinaron que parecía útil, para ingresar las probabilidades máximas de la práctica, buscar cuáles se convierten en los coeficientes extremos en el caso de un viento que varía de 300 Kg en la parte superior a 100 Kg en la superficie del suelo.

Superficies ofrecidas al viento

Las superficies expuestas al viento se determinan suponiendo que el viento normalmente actúa sobre las caras en una dirección horizontal; Lo que equivale a evaluarlos contándolos en su proyección vertical. Las superficies sólidas (pisos, galerías, restaurantes, etc.) se contaron naturalmente en su totalidad. Para la determinación de las superficies rebajadas, hemos admitido que la primera pared normal al viento es totalmente golpeada por él en toda su intensidad y que las paredes vecinas que protege parcialmente también son golpeadas por completo, pero por un viento del cual la intensidad disminuye en la proporción de los vacíos con respecto a la pared anterior. Esto equivale a decir que para la misma intensidad del viento, si s1 y s2 representan las superficies de las piezas encontradas por el viento en la primera y la segunda caras, S1 la superficie de la primera cara que se supone que está completamente llena, tendremos que contar para la segunda cara una superficie de S2 = s2 x (S1 - s1) / S1.

Aplicamos el mismo método para determinar las áreas ofrecidas al viento por las barras de celosía y los puntales que tienen forma de caja y cuyos 4 ángulos de esquina están unidos por una red pequeña. Esta hipótesis ya no es exacta cuando la distancia entre la primera superficie golpeada y la que está detrás se vuelve grande; Porque, como resultado de esta distancia, el viento recupera su intensidad primaria. También en la parte media entre la primera y la segunda plataforma, admitimos que el viento también golpeó todas las cantidades. En la base de la Torre, debido a la gran cantidad e importancia de las piezas de conexión que unen a los ballesteros, fuimos aún más lejos: admitimos que los cuatro postes estaban completos o más exactamente que fueron reemplazados por su proyección completa en el plano vertical y que, además, todos fueron golpeados por igual. Este método de cálculo lleva a casi los mismos resultados que la aplicación de las reglas anteriores, como hemos podido realizar, pero es más sencillo.

División en elementos

En los siguientes cálculos, admitiremos que la acción del viento se concentra en un cierto número de puntos distribuidos adecuadamente en toda la altura de la Torre. Con este fin, dividimos la Torre por planos horizontales en 28 elementos o superficies golpeadas. Cada uno de ellos corresponde a una fuerza del viento que aplicaremos al centro del elemento.

Esta división de la Torre en elementos se indica en la Placa XXXIII. Cada elemento de carrera comprende dos semicaneles adyacentes y, como las alturas de dos paneles sucesivos nunca difieren mucho entre sí, el centro de acción del viento sobre un elemento puede considerarse como situado en el espaciador horizontal que separa los dos paneles; así, en cada uno de estos espaciadores se concentra la mitad de las fuerzas que actúan sobre los dos paneles adyacentes

Superficies de elementos, fuerzas de viento elementales y momentos de reversión correspondientes

Hemos reportado en un apéndice el cálculo detallado de las superficies de cada uno de los paneles y damos en la tabla a continuación las áreas correspondientes a cada uno de los elementos 0 a 28, así como las fuerzas P debidas al viento en las dos hipótesis, obtenidas en Multiplicando las superficies por 300Kg y 200 + 200/300 xh Kilos. Escribiremos en la misma tabla las alturas k del centro de los elementos sobre la base, así como el correspondiente momento de inversión PA.

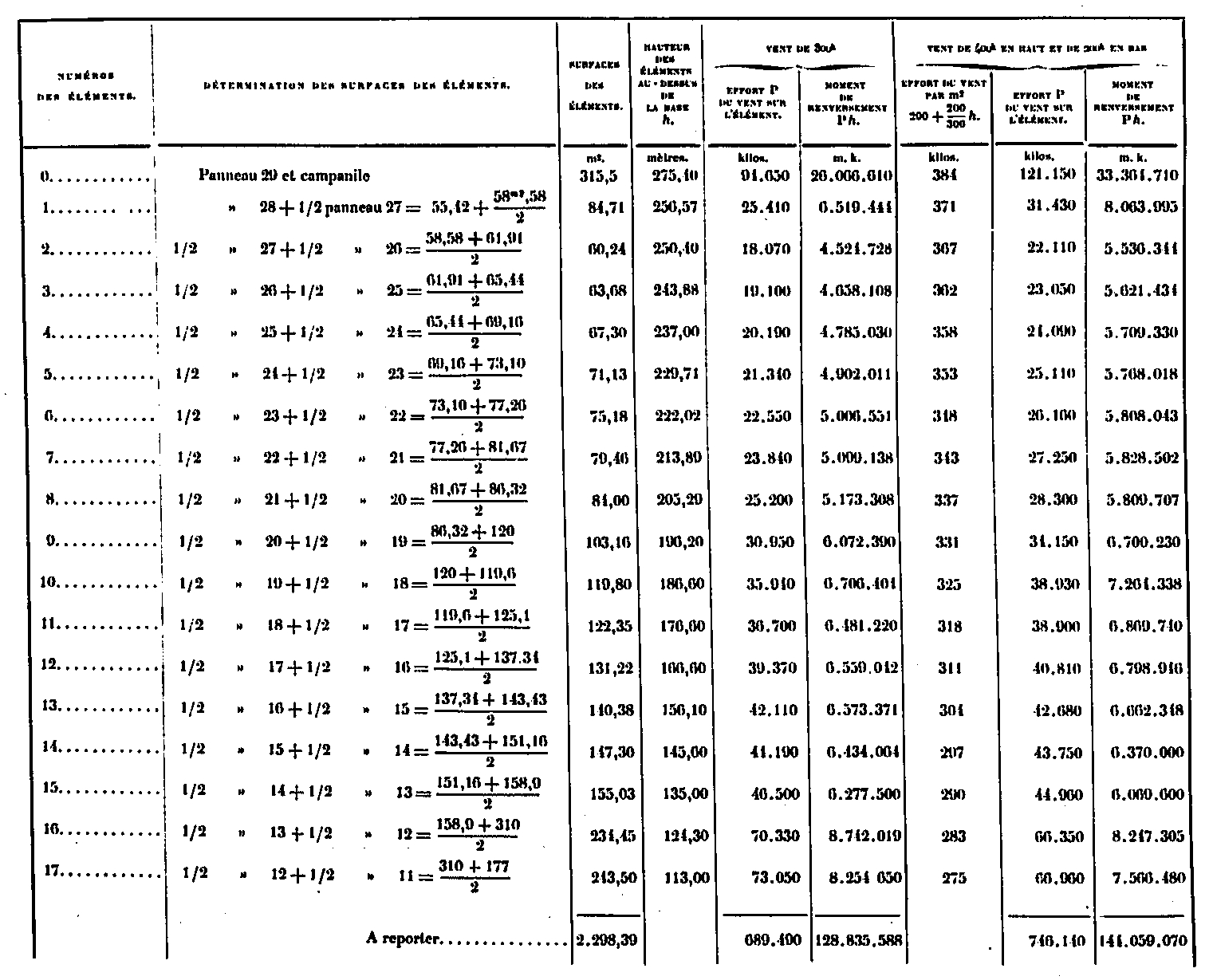
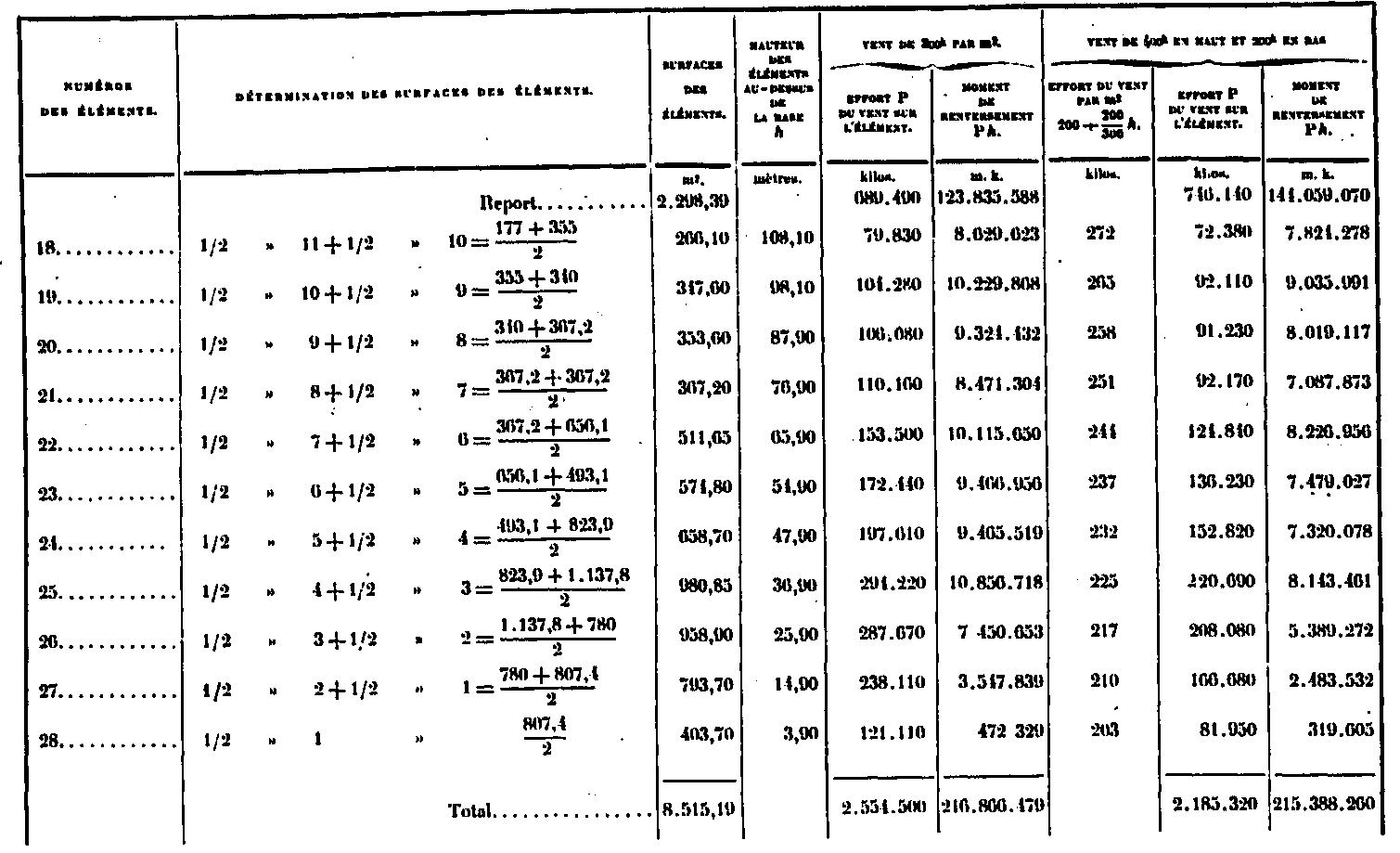
Resulta de esta tabla que toda la Torre tiene una superficie de viento de 8515,19, que el viento, en ambos casos, ejerce esfuerzos que son respectivamente de 2554 toneladas y 2185 toneladas, finalmente, que los momentos de las reversiones totales son respectivamente 216,866 toneladas y 215,588 toneladas-metros; es decir, desde el punto de vista de este efecto, las dos hipótesis son casi equivalentes. En la primera hipótesis, el centro de acción del viento se ubica a una altura de 216 866/2 554 = 84.9m por encima de los soportes; en el segundo 215 388/2 185 = 98.55m

Ahora vamos, conociendo los esfuerzos, para examinar el efecto en cada parte de la Torre. Pero debe considerarse sucesivamente, ya sea la parte superior, es decir, la que se encuentra sobre el segundo piso, en la que todas las cantidades se unen conjuntamente; ya sea la parte inferior, es decir, que va desde el segundo piso hasta el suelo, en la que los cuatro montantes son distintos y solo están unidos por los cinturones de los pisos primero y segundo.

Cálculo de las fuerzas moleculares debidas al viento en la parte superior

Ballesta

Las vigas de cada una de las caras están aseguradas por sus celosías, el cálculo de las fuerzas se realiza simplemente mediante los momentos de flexión.

Sea M el momento de flexión de todas las fuerzas del viento que actúan sobre la sección MN, ω la sección de los 3 ballesteros de la cara golpeada por el viento, o la de la cara opuesta c'c '; e la separación horizontal de los centros de las caras opuestas, y E la fuerza en una cara; el valor de este último será M / e y el coeficiente de trabajo R1 = E / ω, suponiendo que las vigas sean sustancialmente verticales y que las ballestas vecinas de la fibra neutra tengan un momento de resistencia insignificante. Al realizar el cálculo de la región vecina del segundo piso, en la que los ballesteros bd están separados y al introducir el momento exacto de inercia, teniendo en cuenta estos ballesteros, sería fácil reconocer que, incluso en estos puntos, su influencia Es despreciable y solo afecta el coeficiente de trabajo en aproximadamente 0.2 kg.

La curva de los momentos de flexión se traza en la Placa XXXIII, fig. 3, para cada una de estas dos hipótesis, utilizando los polígonos de fuerza, las figuras 1 y 2. Dado que la escala de longitud es de 0,002 por metro y las distancias polares son de 800 000 kilos, los momentos para los momentos son escala de 0.002 / 800 000 = 0.0025 por 1,000,000 kgm. Se pueden leer directamente en el croquis.

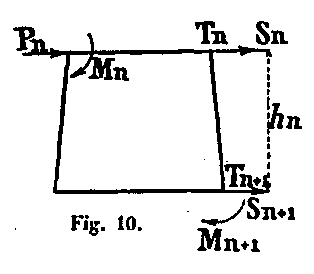
Para calcularlos numéricamente, usamos la siguiente consideración: Deje que dos secciones Sn y Sn + 1, separadas por la altura hn del panel, en la que Mn, y Mn + 1 sean los momentos de flexión, Tn y Tn + 1 sean los Fuerza de corte y Pn es la fuerza del viento en la sección Sn.

Tenemos Mn + 1 = Mn + (Tn + Pn) nn o Mn + 1 = Mn + Tn + hn, lo que permite deducir cada momento del momento anterior, agregando el producto de la fuerza de corte en el punto considerado por el Altura del panel. Así, las cifras en la siguiente tabla de la sección I a la sección XVII han sido establecidas. Como verificación, también hemos determinado directamente para esta sección XVII, el momento de caída correspondiente a cada una de las dos hipótesis; es la suma de todos los momentos parciales debidos a las fuerzas del viento que actúan sobre esta sección; Primero daremos esta imagen.

Cálculo del momento de flacidez en la sección XVII.

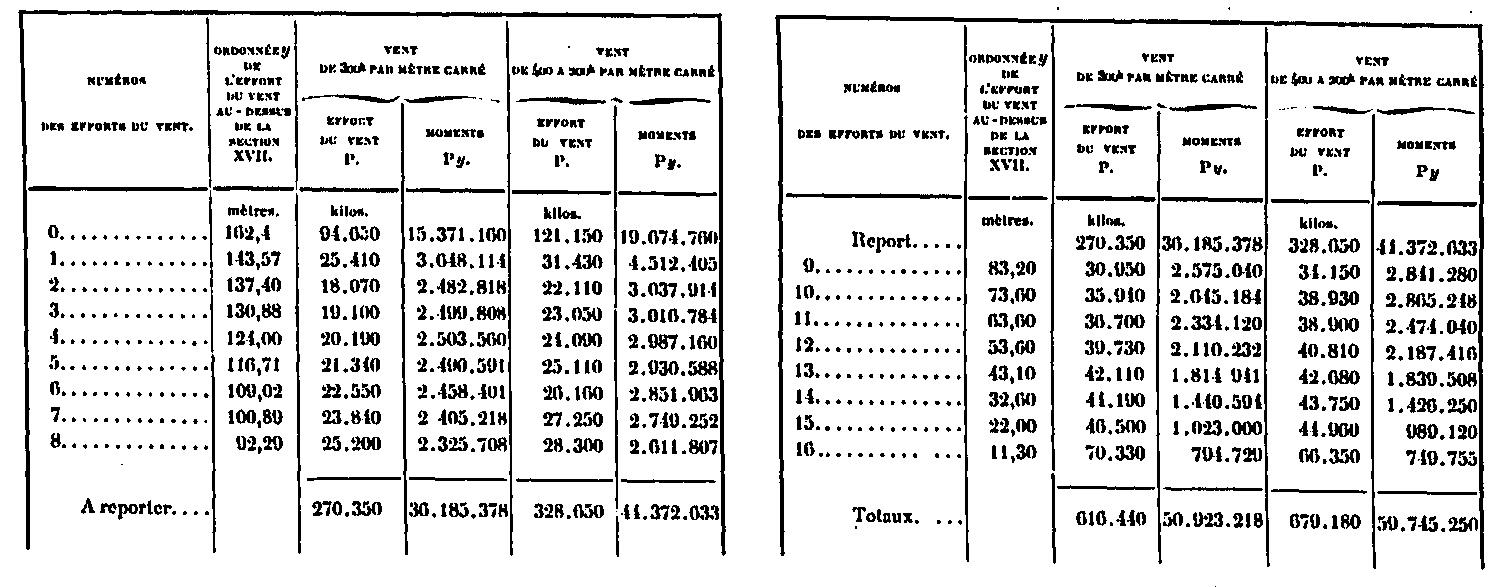
Los momentos en esta sección son 50 923 218m. kg. En la primera hipótesis y 59 745 250m. kg. en el segundo En la siguiente tabla, hemos resumido los elementos del cálculo para cada una de las secciones, como los momentos de flexión y las fuerzas de corte, así como las fuerzas en las caras y los coeficientes de trabajo en las vigas.

Cálculo del momento de flexión, fuerza de corte y coeficiente de trabajo en las vigas para cada una de las acciones anteriores a la sección XVII

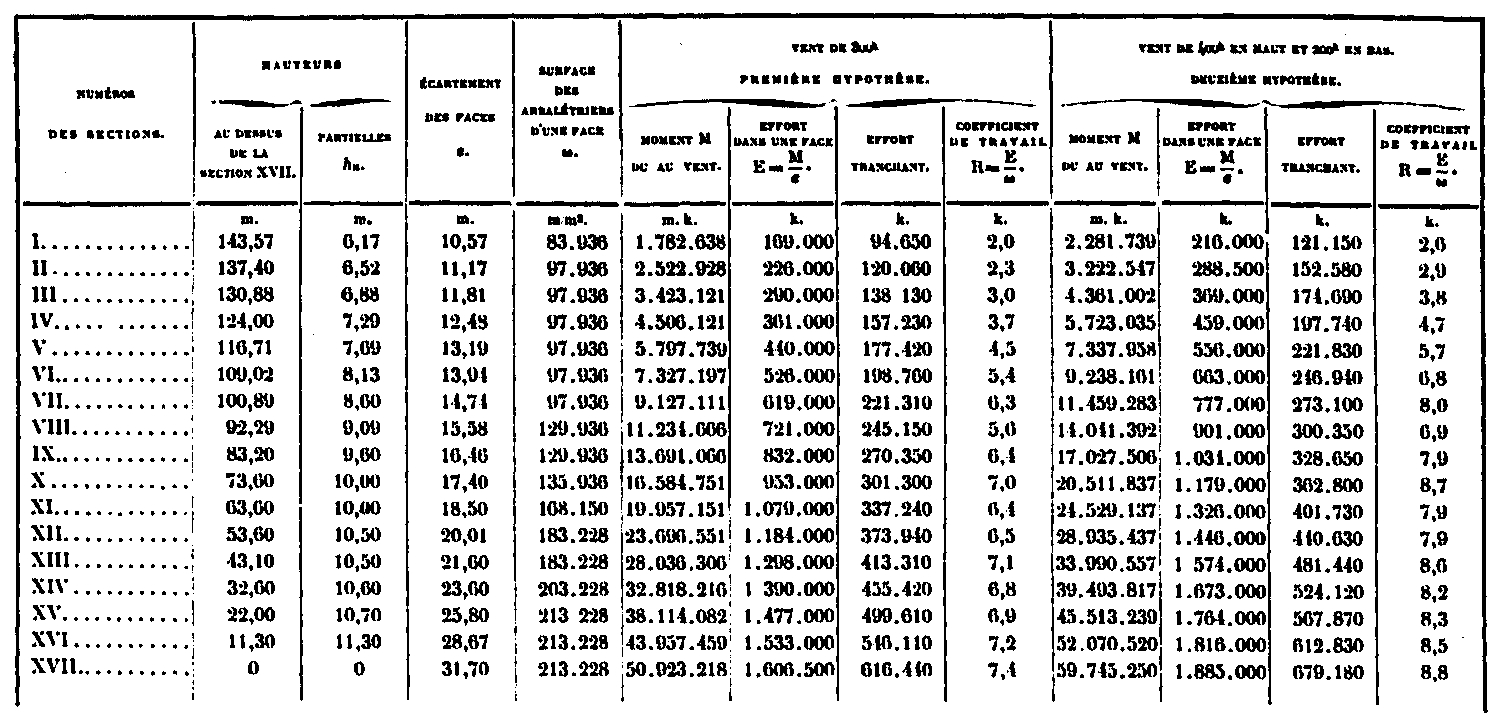
El trabajo máximo debido al viento en las vigas tiene lugar en la sección XVII, donde alcanza los 7.4 kg y 8.8 kg por milímetro cuadrado.

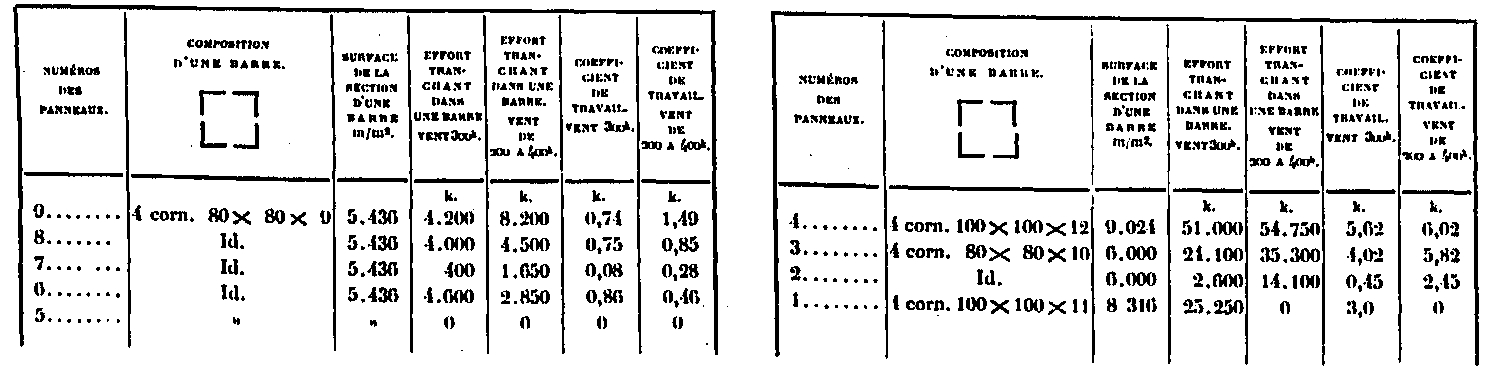
Enrejado

Admitiremos que las fuerzas de las celosías cortadas por la misma sección horizontal MN se distribuyen por igual entre todas las barras de las paredes resistentes. Por lo tanto, calcularemos el esfuerzo F según estas barras como si uno de ellos, por ejemplo, AD, estuviera solo, y dado que el número de barras resistentes es 8, es decir, 4 por pared, se admitirá que el esfuerzo para cada barras es F / 8.

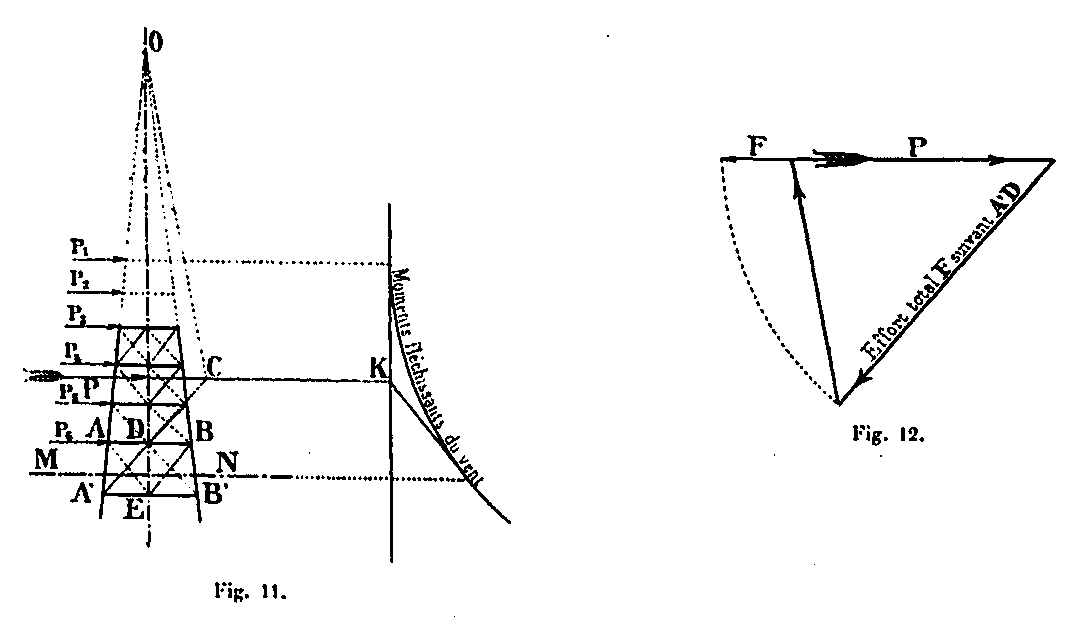
La fuerza F se obtiene descomponiendo la fuerza externa en 3 fuerzas que pasan a través de las vigas A'A, BB 'y las barras A'D.

Para hacer esto (Fig. 11), es suficiente extender las direcciones AA ', BB' a su punto de intersección O, y la dirección A'D al punto de intersección C con la de la resultante de las fuerzas externas P, luego únase a CO y construya el polígono de las fuerzas de la Figura 12; Su línea de cierre paralela a A'D da el esfuerzo F buscado. La posición de la propia fuerza externa P se obtiene para cada sección MN, por medio del polígono funicular de los momentos de flexión debidos al viento (Fig. 11), al determinar la intersección K de su primer elemento vertical con la extensión de la elemento de corte.

Podríamos haber tomado la barra DB 'y hubiéramos obtenido el mismo esfuerzo de manera similar, debido a la simetría de las barras A'D y DB'. En cuanto a las barras AE o EB, se obtendrían esfuerzos ligeramente más altos, pero poco diferentes, por lo que es necesario tenerlos en cuenta; Es por esta razón que consideramos solo la barra A'D y que dimos a otros la misma sección. Por el bien de la figura general, Placa XXXIII, hemos reducido la fuerza F en la dirección de la fuerza P. (Fig. 12). La siguiente tabla da para cada sección, en las dos hipótesis, el valor del esfuerzo F, F el del esfuerzo en cada barra, la sección del mismo y el trabajo correspondiente.

Cálculo de fuerzas y coeficientes de trabajo en barras de celosía sobre la sección XVII

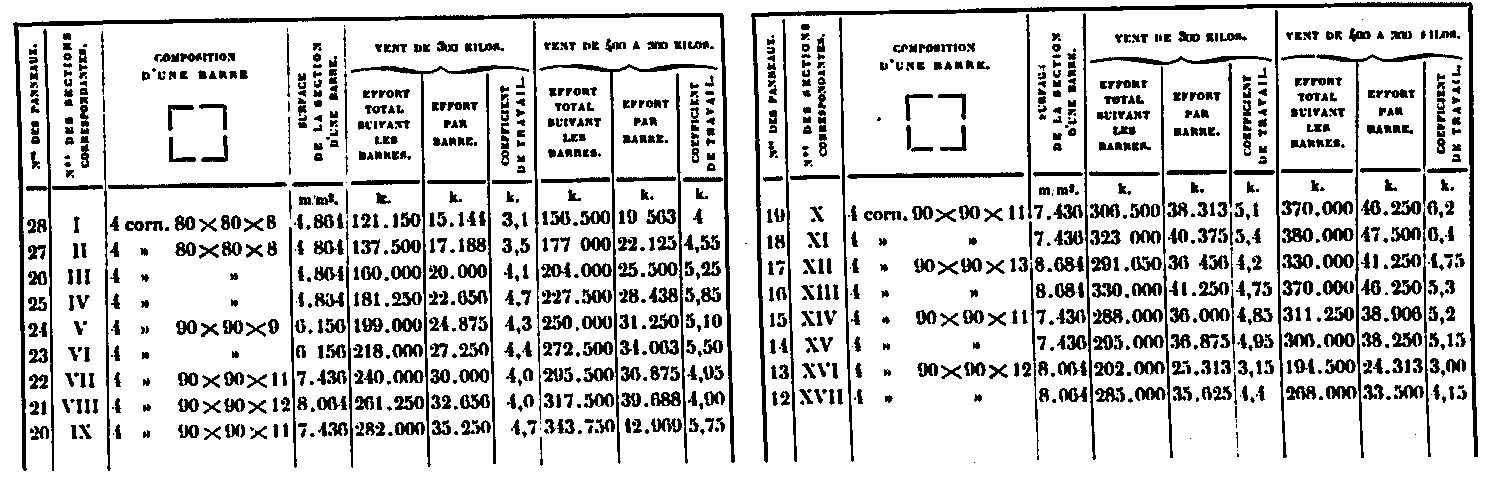
El coeficiente de trabajo promedio es de alrededor de 5 a 6 kilos.

Cálculo de las fuerzas moleculares debidas al viento en la parte inferior

Principios de calculos

Sean P1, P2, P3, ... los diferentes componentes del viento que actúan sobre la Torre en las alturas h1, h2, h3, ... por encima de la base AA '.

Supongamos que trazamos el polígono funicular de estas fuerzas, solo para la parte inferior (Fig. 13), usando el polígono de fuerza (Fig. 14) en el que las fuerzas se transportan horizontalmente y cuya distancia polar es V '.

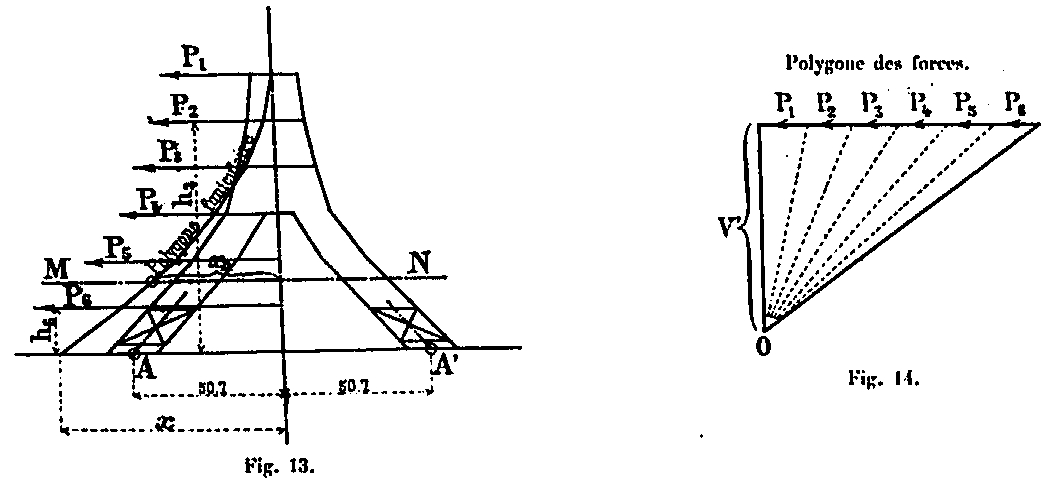
Sea M = ΣPnhn el momento de inversión total de todas las fuerzas del viento P1, P2, P3, ... en relación con la base AA 'de la Torre. El momento en cualquier sección MN es Mn = xnV ', en la base es M = xV', expresiones en las que xn yx representan las abscisas del polígono funicular en la sección MN y en la base (Fig. 13). En cuanto a la distancia polar V, es arbitrario: tener que corresponda al polígono funicular que pasa a través de los soportes, basta con poner M = 50.7 V, siendo 50.7 la abscisa del centro de los montantes en la base; de donde sacamos V = M / 50.7. Este polígono funicular es entonces al mismo tiempo la curva de las presiones de las fuerzas del viento.

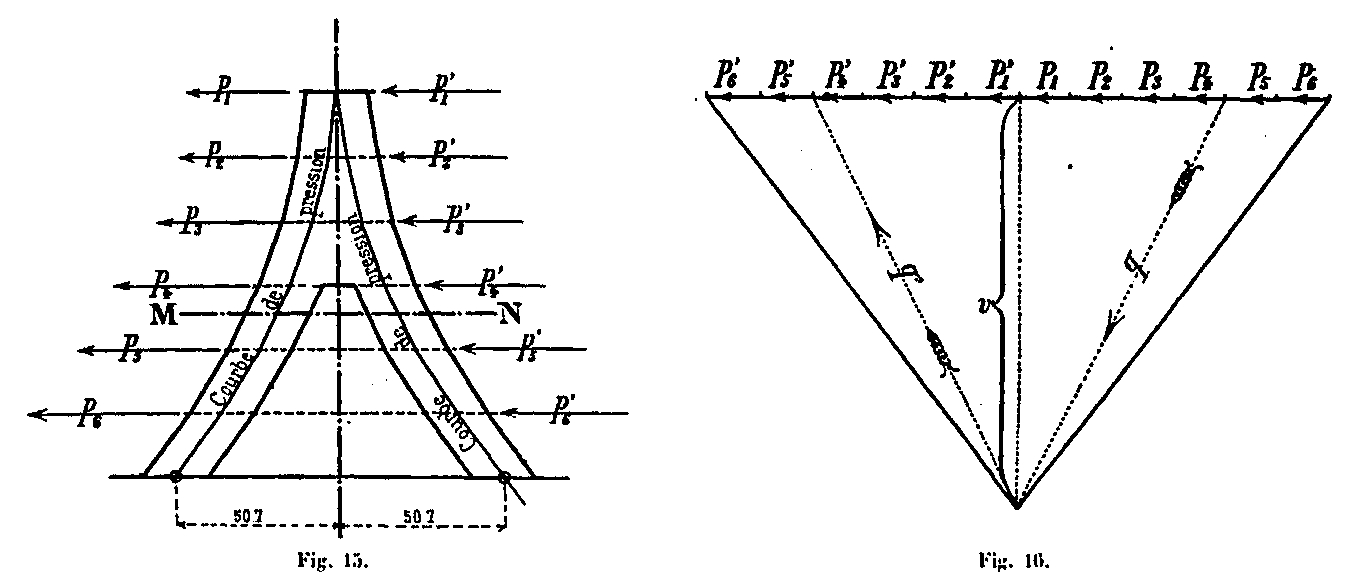
Como solo determinamos los esfuerzos por una sola cantidad, es más fácil transportar las fuerzas poligonales, en lugar de los esfuerzos totales P, una cuarta parte de estos esfuerzos para obtener el esfuerzo directamente en una cantidad.

La curva de las presiones correspondientes a estas fuerzas ρ1 = P1 / 4, ρ2 = P2 / 4, etc., se debe trazar con una distancia polar v = V / 4 (Figuras 15 y 16).

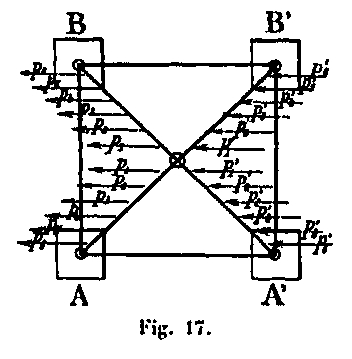
Para una sección MN (Fig. 15), la fuerza externa q en una posición vertical se da en el polígono de fuerza (Fig. 16). Las fuerzas en los montantes son las fuerzas de tensión q en las dos primeras cantidades A 'y B' golpeadas por el viento, y las fuerzas de compresión simétricas q en los otros dos montantes A y B (Fig. 17). Solo consideramos las cantidades en que el viento produce fuerzas de compresión además de las producidas por el propio peso de la construcción. La fuerza externa q producida en la sección MN:

Una N fuerza de compresión que actúa en la fibra media de la cantidad.
Una cizalla T normal a esta fibra media.
Momentos de flexión por el hecho de que la curva de presión no pasa en esta sección en el mismo punto que la fibra promedio, es decir, por el eje de la cantidad.

Esfuerzos de compresión y fuerzas de corte

Estas fuerzas se obtienen para cada sección al descomponer en las fuerzas poligonales (Fig. 18) la fuerza externa q en dos fuerzas, una OC paralela a la dirección de la fibra promedio en la sección MN, la otra CD normal a esa misma dirección.

Este esfuerzo de CD es la fuerza de corte T que se descompondrá de acuerdo con las direcciones de las barras de celosía del panel cortado por la sección MN; Así tendremos el esfuerzo producido por el viento en estas barras.

En cuanto a la fuerza de compresión OC, a medida que la cantidad se inclina a lo largo del plano diagonal de la Torre, esta fuerza que actúa en un plano vertical aún debe descomponerse en la dirección del montante vertical en la cara perpendicular a la figura (Fig. 18 ). Esta descomposición se puede hacer de la siguiente manera:

Desde el polo O del polígono de fuerza como centro, dibujamos un arco arbitrario desde el punto 1 ubicado en la vertical del polo hasta el punto de encuentro K con OC. Desde el punto K, elevamos un KL perpendicular a OC y el punto I, un IL perpendicular a KL; Así obtenemos el punto L, intersección de estas dos líneas. Al descomponer el componente OC en la dirección de OL, se obtiene la fuerza de compresión N * = OE en la cantidad. El ángulo del CEO es de hecho igual al ángulo de inclinación de la fibra promedio en una de las caras de la vertical.

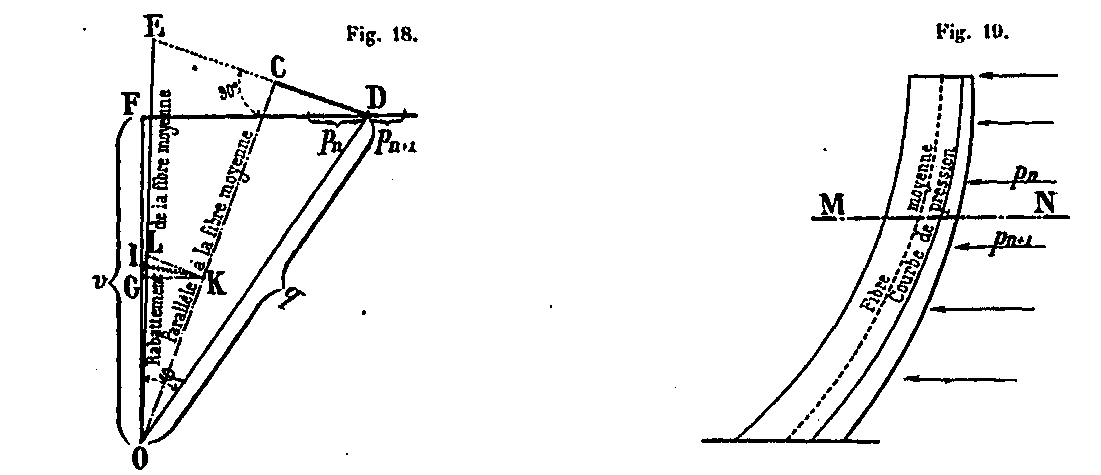
De hecho, como MN es un plano horizontal (Fig. 20), para tener OL, sabiendo OK, es suficiente tener la longitud KL = KG y llevarla en un perpendicular a OK elevado al punto K. Ahora, como Hemos demostrado anteriormente que, con respecto a las cargas verticales, G está en el horizontal dirigido por K, y KG reducido a KL da el punto L buscado (Fig. 18). Vemos inmediatamente que la construcción indicada arriba, por medio de las perpendiculares KL e IL, se reduce a ésta; define gráficamente el punto L muy exactamente. Esta fuerza N, que actúa en el centro O de la cantidad en la sección MN, se distribuye por igual entre las cuatro vigas a, b, c y d (Fig. 21) y proporciona en cada una de ellas una fuerza de compresión E1 = N / 4 .

Las curvas de presión correspondientes a los dos casos de sobrecarga de viento se han trazado en el diagrama de la Placa XXXII, fig. 3, utilizando los polígonos de fuerza fig. 1 y fig. 2, que se han determinado sólo para las secciones de la parte inferior. La distancia polar de cada uno de ellos es igual a un cuarto del momento de inversión M dividido por la media separación de los montantes en la base, o 50.70 m. En la primera hipótesis, hemos visto que el momento de reversión es de 216 866 479 m. k. Por lo tanto, vn = 1/4 x 2/866 479 / 70.70 = 1069 350 kg.

En la segunda hipótesis, el momento de reversión es 215 388 260 m. k. y la distancia polar es vn = I / 4 × 215 388 260 / 50.70 = 1 062 050 Kg. Las fuerzas de corte también se determinan en los mismos polígonos.

Momentos de flexión

La pareja que los produce puede descomponerse en dos; una μ actuando en un plano paralelo a la dirección del viento XY, la otra μ 'actuando en un plano perpendicular ZU (Fig. 22). El primero se debe a la desalineación de la fuerza externa en la dirección de la dirección del viento, y el segundo a la desalineación en la dirección normal a la dirección del viento, como se muestra en las Figuras 23, 24, 25 y 26 a continuación. a continuación.

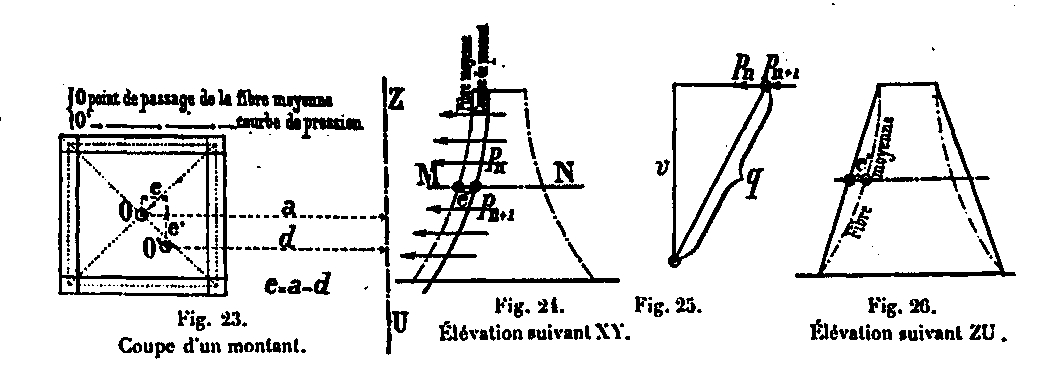
Determinación de momentos paralelos a la dirección del viento

Para la determinación de estos momentos, es necesario tener proyecciones de la curva de presión en los planos XY y ZU. El primero viene dado por el polígono funicular (Fig. 15, p.34) correspondiente a las fuerzas de inversión horizontal (Placa XXXII, Fig. 3). Al llamar la distancia horizontal de esta curva de presión desde la fibra promedio para cualquier sección MM '(Fig. 27), el momento de flexión de la fuerza externa F es igual a Fθ, donde θ es la distancia normal: siguiendo triángulos similares formados con el polígono de fuerza, e / θ = F / v, entonces Fθ = ve. Designaremos este momento en el plano vertical mediante μ, por lo que tendremos μ = ve.

Este momento debe ser proyectado de acuerdo a la cara de la cantidad. Para eso, es suficiente representar el momento μ, actuando en el plano XY, por su eje representativo y componerlo con el momento μ buscado, cuyo eje es perpendicular al plano de la cara B de la cantidad; así tenemos μ1 = μ / sin α, donde α es la inclinación de la cara de la vertical en la horizontal (Fig. 28).

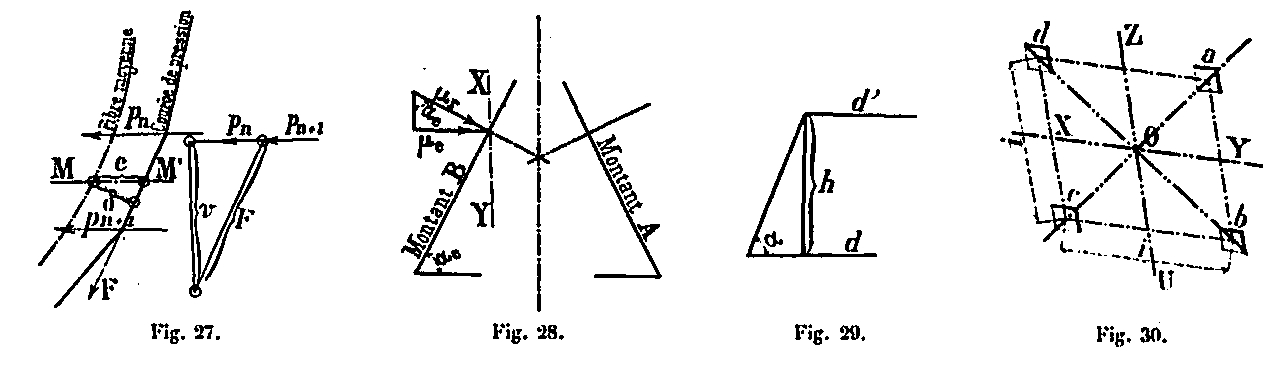
Es fácil calcular la expresión μ / sin α. De hecho e = a - d (Fig. 23), es la diferencia entre la abscisa de la fibra promedio, con respecto al eje vertical en el plano vertical de los montantes, dada por el diagrama de la elevación (Placa XXXI) y la abscisa de la curva de presión que se calcula utilizando los momentos de inversión. Como M = dv, obtenemos d = M / v.

Los valores de M se calculan numéricamente usando la tabla anterior, como hicimos para la parte superior, por las mismas fórmulas Mn + 1 = Mn + Tn + 1 + hn. En cuanto a los ángulos α, se determinan en el mismo diagrama de la elevación por su tangente (Fig. 29): siendo h la altura del panel cuyos d y d 'son las abscisas, tg α = h / (d - d' ) de donde uno deriva los valores de sin α.

Finalmente, v es la distancia polar, igual a V / 4, de los polígonos de fuerza (Placa XXXII, Figs 1 y 2).

En cuanto a la fuerza producida en las vigas bajo la acción del momento μ, es igual para una cara que E = I / 2 x μ / i, que denota el espaciado normal de las vigas en sus caras plegadas (Fig. 30) . La siguiente tabla resume todos los elementos para ambas suposiciones.

Cálculo de las fuerzas en las vigas debido a los momentos de flexión que actúan en el plano paralelo a la dirección del viento.

Con respecto a los signos, siempre damos el signo positivo a las parejas que giran alrededor del centro O de la cantidad en la dirección de las agujas del reloj. Para un valor positivo de μ, este valor de E es una compresión en la viga a y una fuerza de tensión en la viga c, tanto cuando el viento está actuando en la dirección XY como cuando está actuando en la dirección UZ.

Por otro lado, para las vigas b y d, la fuerza En representa tensión o compresión, dependiendo de si el viento está actuando en una u otra de estas direcciones. Por ello tenemos, suponiendo positivas las fuerzas compresivas:

En el arquero a, un esfuerzo + E = μ / 2i
En la ballesta c, un esfuerzo - E = μ / 2i

Cuando el viento actúa en la dirección XY, tenemos:

En el arquero b, un esfuerzo + E = μ / 2i
En la ballesta d, un esfuerzo - E = μ / 2i

Cuando actúan en la dirección UZ, las fuerzas en estos dos ballesteros cambian su signo.

Determinación de momentos normales en dirección del viento

Las fuerzas debidas a los momentos de flexión transversales se determinan de manera análoga.

El momento de flexión μ de la sección MN, producido por la desviación de la fuerza externa en el plano vertical UZ normal al viento, es igual al producto de la distancia polar v del polígono de fuerza por el espaciado horizontal e 'de la fibra promedio y la cuerda (fig. 26); es decir, tenemos μ = ve '; Este momento actúa en el plano vertical UZ.

Para obtener el momento correspondiente plegado en la cara, haremos una descomposición similar a la que ya se ha hecho para el par de torsión del plano XY paralelo a la dirección del viento. Por lo tanto, nos encontramos ante la cantidad de un momento que es igual a μn '= μn' / sin αr y que produce en los ballesteros a, b, c, d esfuerzos Eα = μ '/ 2i. Estos esfuerzos son siempre positivos para el arquero, y negativos para el arquero c, asumiendo que son positivos. Es decir, tenemos:

En el arquero a, un esfuerzo + E = μ / 2i
En la ballesta c, un esfuerzo - E = μ / 2i

Cuando el viento actúa en la dirección XY, tenemos:

En el arquero b, un esfuerzo + E = μ / 2i
En la ballesta d, un esfuerzo - E = μ / 2i

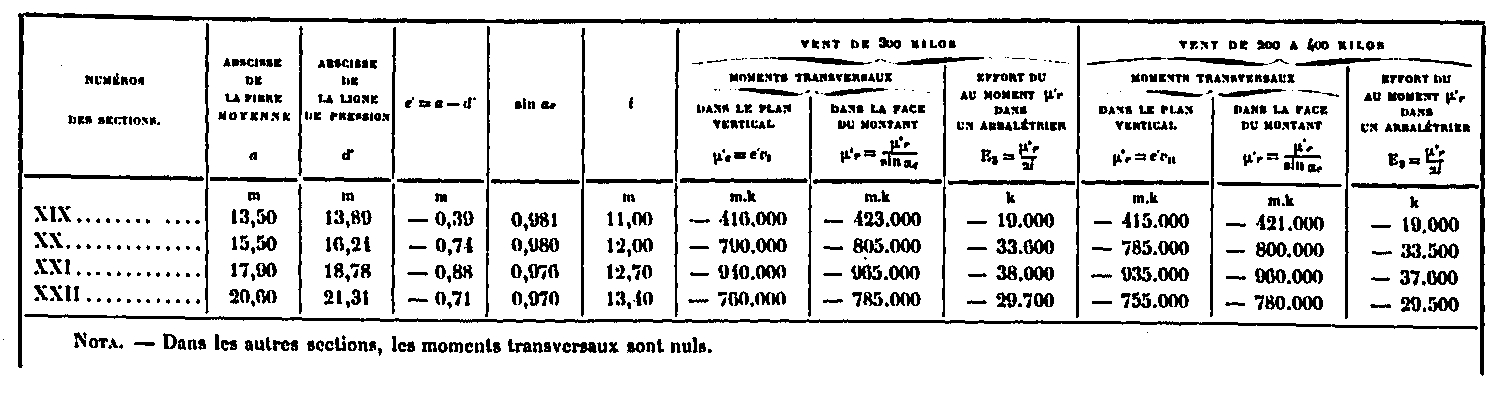
Cuando él actúa en dirección a UZ, los esfuerzos en estos dos últimos ballesteros cambian su señal. Estos momentos se calcularon para las secciones XIX, XX, XXI y XXII en la tabla a continuación mediante el método que acabamos de indicar. En todas las demás secciones, son nulas. En la dirección normal al viento, los esfuerzos se transmiten de acuerdo con la cuerda de la fibra promedio entre dos correas. La abscisa d de esta cadena, así como la abscisa de la fibra promedio, se muestran en la figura 31 de arriba y se encuentran en la tabla que también da los valores e '= a - de los de sin α, de i, así como los momentos μ '= év y μ' = μ '/ sin αn que corresponden a las dos hipótesis de sobrecarga de viento, y las fuerzas En = μ' / 2i.

Cálculo de las fuerzas en las vigas debidas a los momentos transversales.

Cálculo de fuerzas de viento totales en ballesteros y coeficientes de trabajo máximos

Ahora tenemos todos los elementos para resumir las fuerzas totales en las vigas, es decir, las fuerzas longitudinales que siguen la fibra promedio y las fuerzas debidas a la desalineación del par. Estos esfuerzos, asumiendo los momentos positivos μn y μn ', son:

En el ballestero un esfuerzo E4 = E1 + E2 + E3
En la ballesta c, una fuerza E4 = E1 - E2 - E3

Cuando el viento actúa en la dirección XY, tenemos:

En la ballesta b, una fuerza E4 = E1 + (E2 - E3)
En la ballesta d, una fuerza E4 = E1 - (E2 - E3)

Cuando el viento actúa en la dirección UZ, tenemos:

En la ballesta b, una fuerza E4 = E1 + - (E2 - E3)
En la ballesta d, una fuerza E4 = E1 + (E2 - E3)

Como el viento puede actuar en una cara o en la otra, elegiremos el caso que dé en las vigas b o los mayores esfuerzos, que son por lo tanto de:

EN = E1 + (E2 - E3) si E2 - E3 >0
EN = E1 - (E2 - E3) si E2 - E3 <0

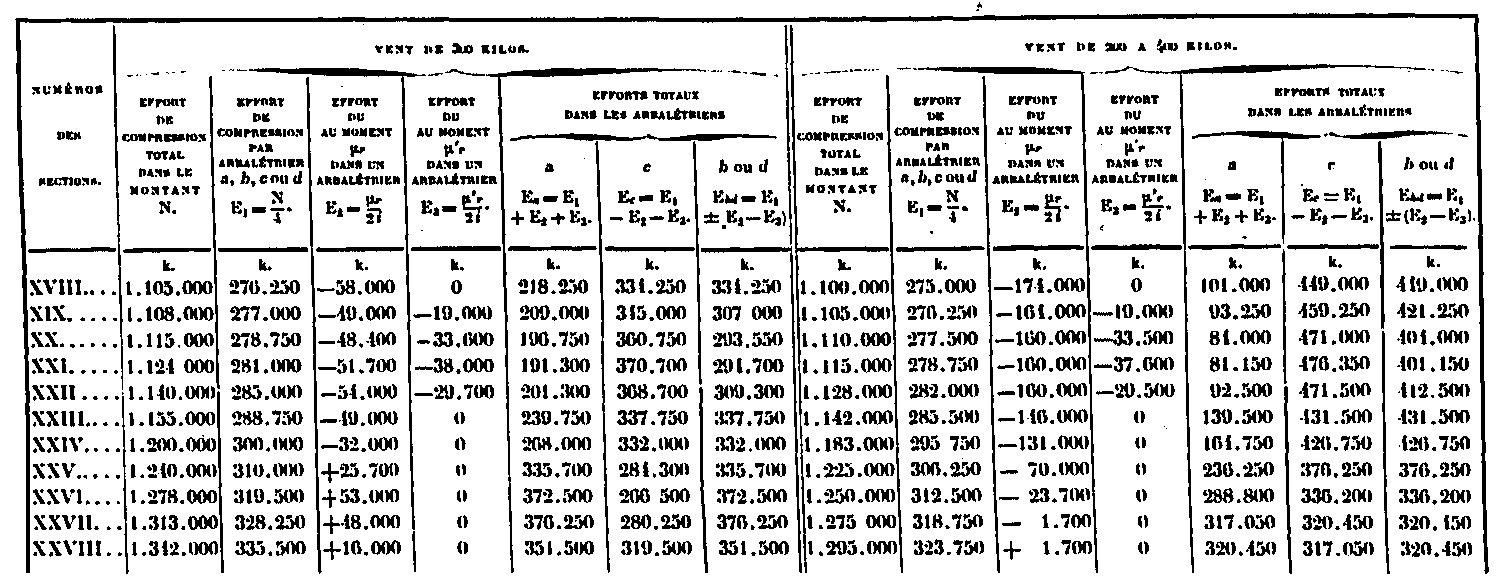
Estos esfuerzos se resumen en la tabla a continuación para ambas suposiciones.

Cálculo de las fuerzas totales debidas al viento en las vigas.

Es fácil deducir el coeficiente de trabajo de las vigas, cuya sección se conoce; Esto es lo que nos da la siguiente tabla:

Cálculo de los coeficientes de trabajo máximos debidos al viento en las vigas.

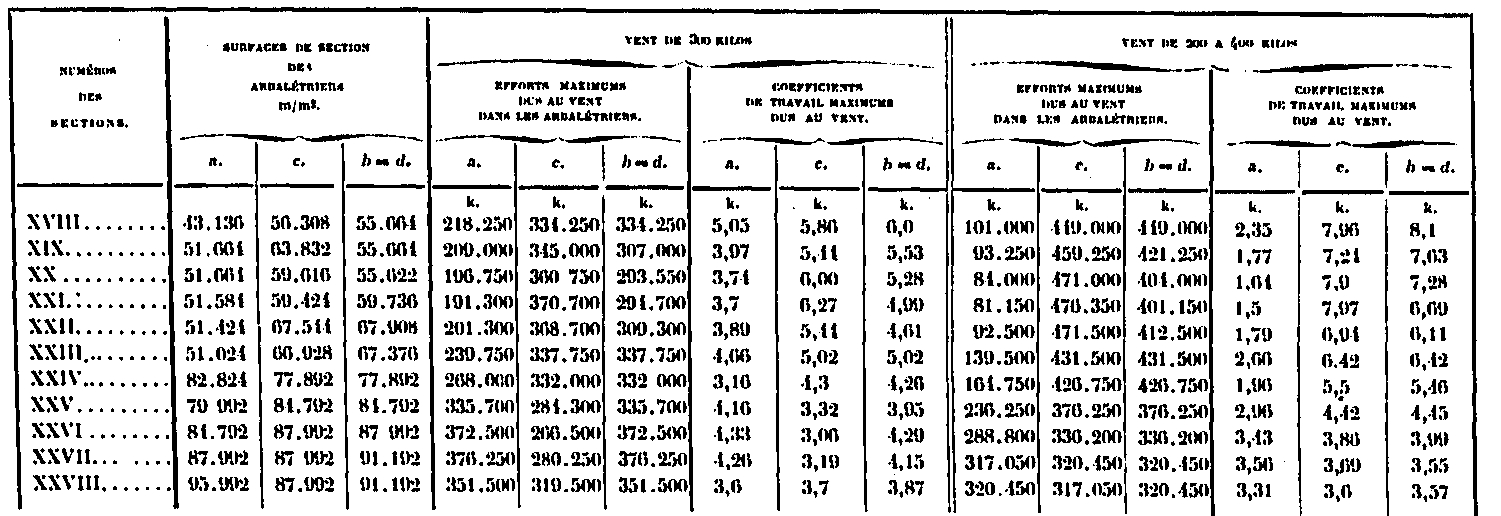
Estos coeficientes deberán sumarse a los debidos a los propios pesos.

Cálculo de las fuerzas debidas al viento en las barras de celosía y coeficientes de trabajo correspondientes

Estos esfuerzos, junto con los coeficientes de trabajo correspondientes, se resumen en la siguiente tabla:

Hemos admitido en los cálculos anteriores la hipótesis de un viento que golpea la Torre normalmente en una de sus caras; Ahora examinaremos el caso de un viento que actúa en cualquier dirección y mostraremos que las fuerzas que produce son iguales o inferiores a las ya calculadas. Para este propósito, considere un prisma cuadrangular ABCD de ancho a, y una altura igual a la unidad (Fig. 52).

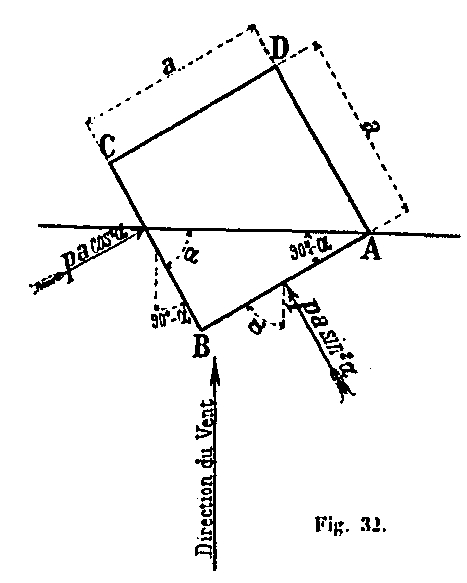
Si un viento de intensidad p actúa normalmente en una de sus caras, produce en el prisma una fuerza pa. Cuando, por el contrario, el viento se encuentra con la cara AB del prisma en un ángulo α, produce en esta cara una fuerza normal que tiene el valor pa sin α. La fuerza correspondiente del viento en la cara CB es igual a pa cos α.

Entonces, si P1, P2, ... Pn representan las fuerzas del viento que actúan sobre la Torre normalmente en una de sus caras, un viento de la misma intensidad, que llega a golpear la cara AB en un ángulo α, producirá en esta cara Fuerzas P1 sen α, P2 sen α, etc. y en la cara normal CB de las fuerzas P1 cos2 α, P2 cos2 α, ... Pn cos2 α.

Bastará, por lo tanto, examinar por separado las fuerzas producidas por las fuerzas P2 sen α normales a la cara AB y las dadas por las fuerzas P cos2 α normales a la cara BC, para luego sumarlas y tener las fuerzas Totales por el viento.