Cálculo de fuerzas debido al peso

¿Cuáles son las cargas verticales?

Las cargas verticales, utilizadas en el cálculo del marco general, incluyen solo el peso propio de la construcción. Es bastante inútil incluir el peso de los visitantes; Se ha tenido en cuenta solo en el cálculo de habitaciones especiales, como pisos.

De hecho, la violencia de los vientos que hemos admitido para llegar a la determinación de la resistencia de los diversos elementos de la Torre, es tal que haría que la permanencia de la Torre sea absolutamente imposible para cualquier visitante, y por otro lado, El peso de estos visitantes da lugar a una fatiga casi insignificante, en comparación con el peso de la construcción y los grandes huracanes. Si duda de este cálculo, de hecho, se ha realizado, puede consultarlo en esta página, que proporciona el cálculo del peso máximo de visitantes a la Torre Eiffel.

1. Superestructura metalica

La declaración general de las facturas de correo de las planchas y planchas que entran en el armazón de metal de la Torre es de 7 541 214 kg, que incluye:

Este peso no incluye:

Por el momento, solo nos ocuparemos de la primera de estas cifras.

Al contar todos los conocimientos de embarque, para deducir el peso de la superestructura propiamente dicha y al dividir, en cada capítulo, el peso de los remaches colocados en el lugar, estos resbalones se resumen a continuación:

El peso de la superestructura en sí se desglosa de la siguiente manera :

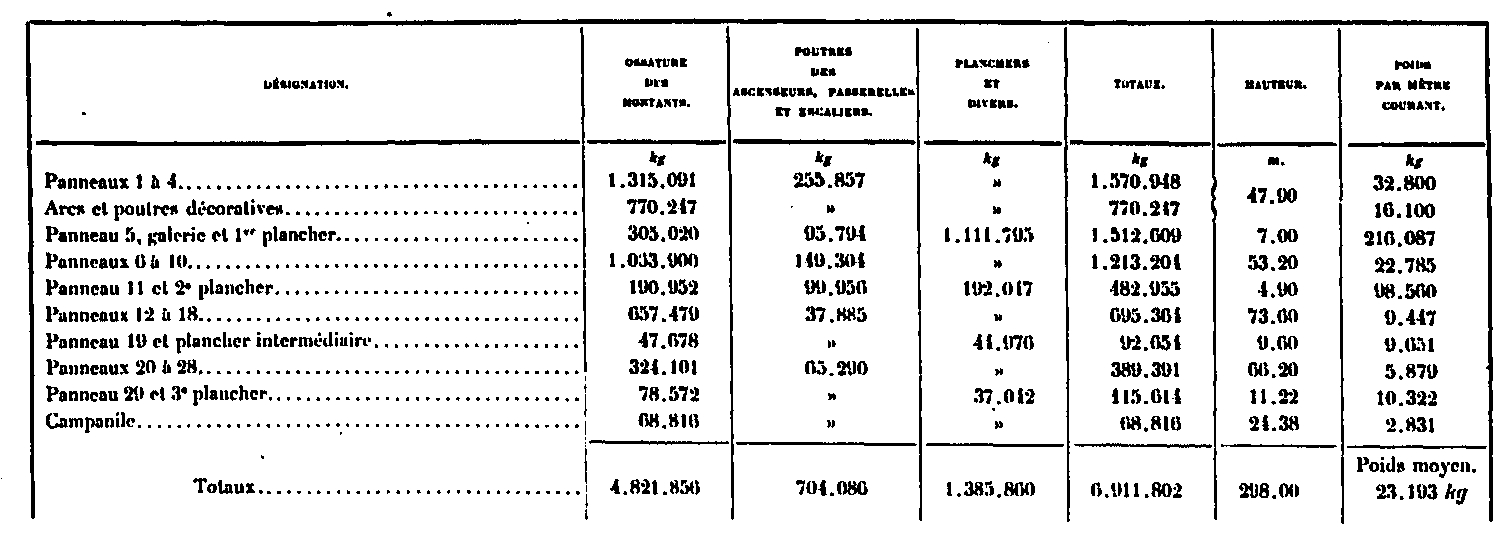
Las cifras en esta tabla se resumen a continuación:

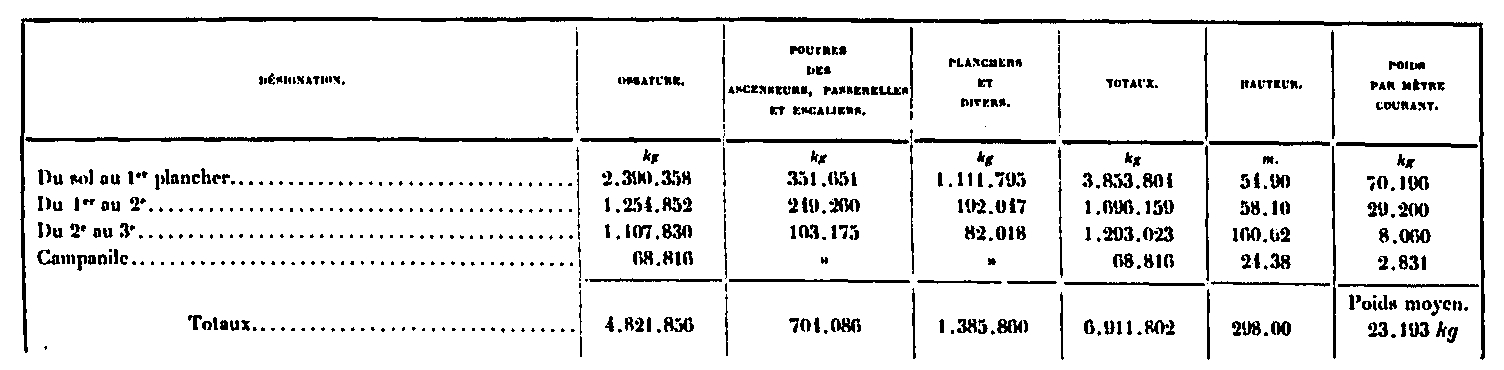
Los pesos que, aparte de la superestructura metálica propiamente dicha, deberán incluirse en los cálculos, son los de los mecanismos y accesorios de los ascensores, así como los de los edificios y el subsuelo de las plataformas. Los estudiaremos por separado.

2. Ascensors

Tienen las siguientes ponderaciones, que se detallarán en el capítulo que se les dedicará:

Al analizar la distribución de estas diferentes cargas de acuerdo con las diferentes partes de la Torre, llegamos a la siguiente tabla:

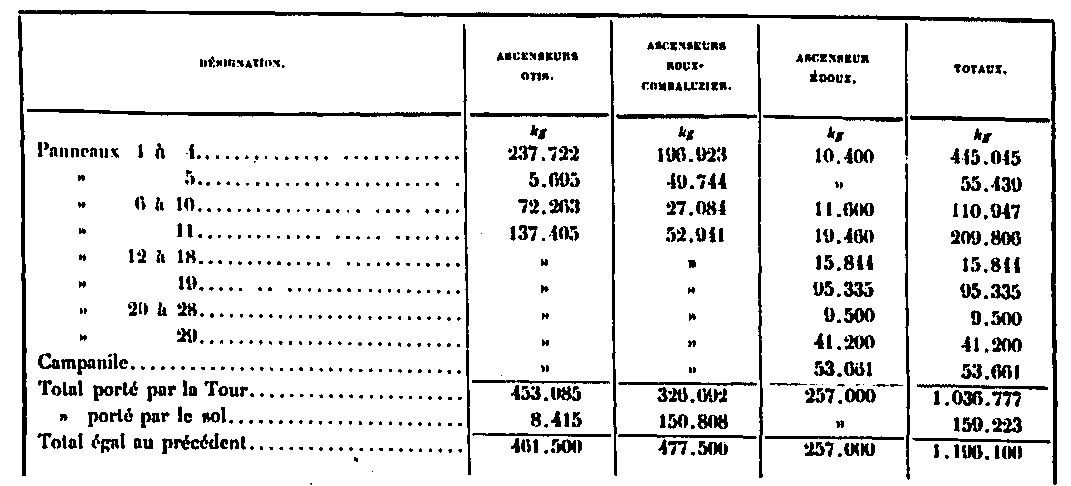
3. Varias instalaciones y plataformas

a. En el campanario, el pabellón comprende:

b. En el panel 29 y en el tercer piso, es necesario contar:

c. En el panel 19 y en el piso intermedio, solo se contabilizarán el piso y los mamparos de la sala del maquinista, cuyo peso es de 2.600 kg.

d. Para el panel 11 y la segunda plataforma tomaremos:

e.En el panel 5 y la primera plataforma, se encuentran los pesos más importantes:

Las cargas debidas a diversas instalaciones y plataformas, son por lo tanto:

El conjunto de cargas verticales que actúan en los diferentes paneles se resume en la siguiente tabla:

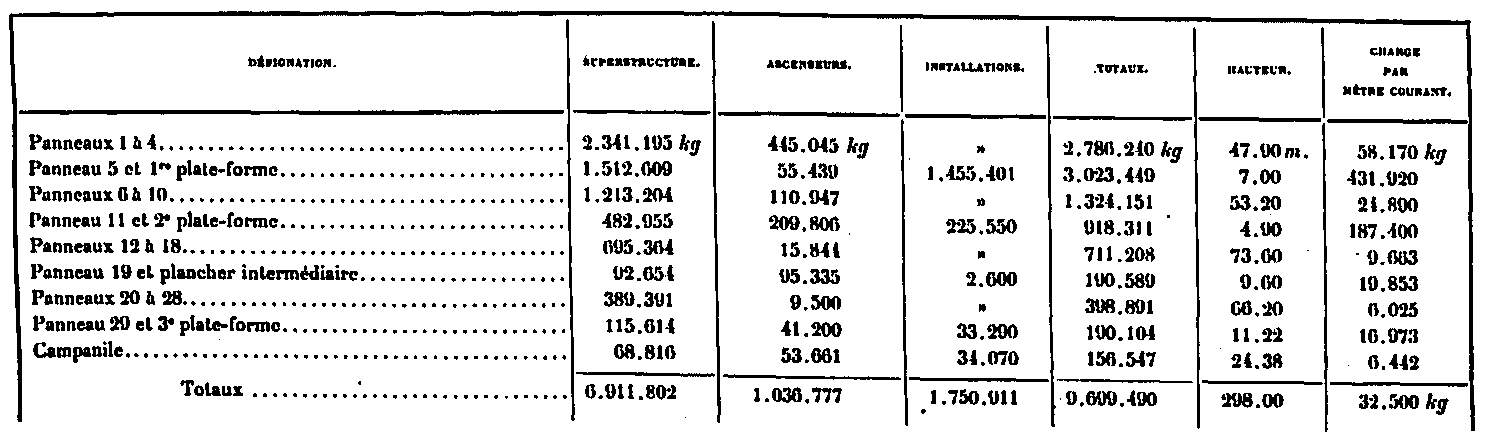
Esta carga de 9,700 toneladas, que es el peso total de la Torre, es la adoptada en los cálculos. El peso de los paneles intermedios no especificados se deduce de su altura y el peso por métrica actual correspondiente.

¿Podría haber sido la torre más alta?

Este capítulo responde a esta pregunta considerando la adición del peso que representaría una elevación adicional de la torre. Si tomamos, en las tablas anteriores, solo el peso del marco, es decir, el peso de los montantes y el de las vigas del cinturón, después de deducir los pisos y las vigas de los ascensores, estos pesos son los siguiente :

Los pesos de la superestructura de metal, dados anteriormente, se pueden resumir en el diagrama de abajo, en el que las partes cortadas representan las cantidades de metal utilizadas en la Torre. La curva en líneas continuas se refiere a los pesos por metro de carrera, relacionados con la construcción en su conjunto. Que en líneas discontinuas es relativo al marco de los montantes, incluidas las vigas de las correas, después de la deducción de los pisos y los ascensores.

Fuerzas de la torre Eiffel

×Cerca

Fuerzas de la torre Eiffel

Fuerzas de la torre Eiffel

Vemos que estos pesos aumentan muy rápidamente con la altura. Podemos inducir cuál habría sido el peso aproximado de la Torre si se hubiera extendido 50 m, es decir, si se le hubiera dado una altura de 350 m.

El peso de los paneles 1 a 4, sin las vigas decorativas, y para una altura de 47 m desde los soportes, es de 1,315,091 kg, o por medidor de corriente de 27,500 kg. El de los paneles 6 a 10 es, para una altura de 53.20 m de 1 063 900 kg, o por metro de corriente de 20 100 kg. De ello se deduce que si la torre tuviera una altura de 50 m más, es decir, si hubiéramos adaptado a la parte inferior un piso de 50 m, el ancho en la base habría sido 150 M aproximadamente, y el peso de este piso habría sido, como marco de las cantidades, 35 000 kg por metro de corriente aproximadamente. El peso adicional correspondiente es de 35,000 x 50 = 1,750,000 kg.

En cuanto al peso de las nuevas vigas de las correas y el panel a esta nueva altura, habría sido 43700 x 100/53, es decir 82 500 Kgl, que para una altura de 10 m da 825 000 Kg, sin incluir los pisos, ascensores, etcétera Por lo tanto, el peso total de la etapa superadded habría sido de al menos 1,750,000 + 825,000 = 2,575,000 kg. El peso comparativo de la construcción es el del marco de los montantes (4,821,856 Kg) menos el de las vigas decorativas (77,247 Kg), o 4,051,609 Kg. Así, para un aumento de altura de 50/300 = 17 %, ¡el peso aumentaría en 2,575,000 / 4,051,000, o 63.5%!

Así calculado, parece obvio que no era necesario escalar la torre más allá de los 300 m, excepto para tener la capacidad de aumentar el gasto de alrededor de 3 millones de francos en ese momento, según una estimación de Gustave. Eiffel.

Cargas verticales que actúan en secciones

De las tablas anteriores, es posible deducir la carga debida a cada uno de los paneles, aplicando, proporcionalmente a su altura, la carga por medidor de corriente en relación con las diversas categorías admitidas. Estos cargos son los siguientes:

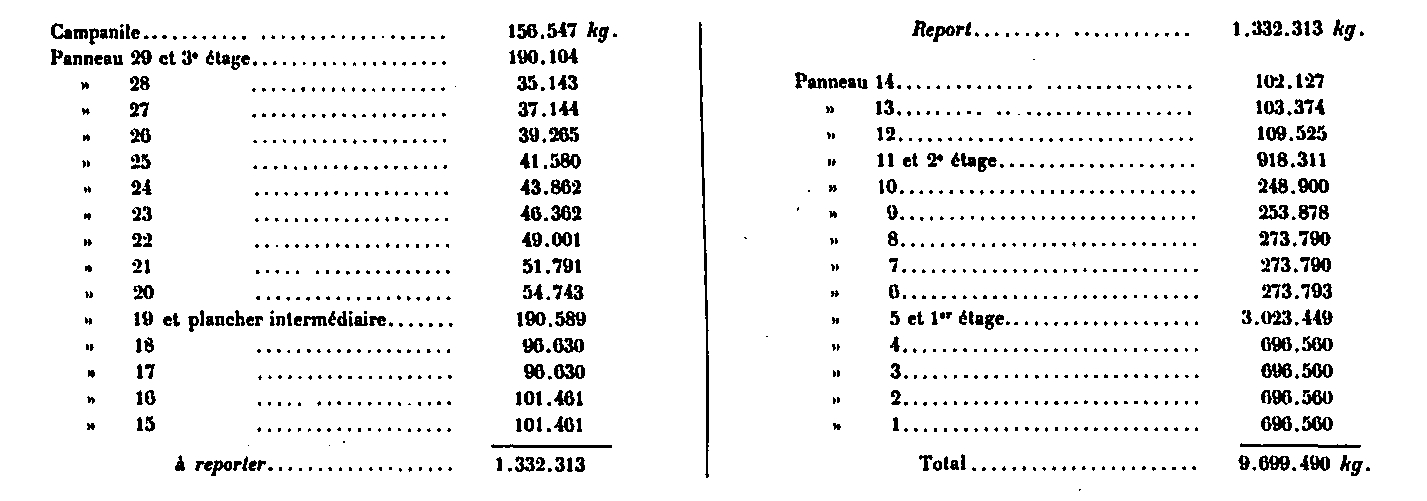
Aunque los cálculos de la Torre se hicieron con el peso total anterior, las diferencias en la distribución de las cargas, especialmente con respecto a los ascensores, habían dado lugar a cifras algo diferentes para las cargas en cada sección. Sin embargo, en vista de estas diferencias, nos ha resultado bastante inútil hacer estos arduos cálculos nuevamente, debido a que estas diferencias parciales no tienen una influencia apreciable en el valor de los coeficientes del trabajo. Solo tienen importancia en la parte superior de la torre. Ahora, se verá más adelante que en esta parte la influencia del viento es muy predominante sobre la de las cargas; además, en los paneles 12, 13 y 14, donde el coeficiente total de trabajo es bastante alto, la influencia de las diferencias informadas puede considerarse absolutamente cero.

Por lo tanto, podemos, sin ningún inconveniente, mantener los cargos a continuación, adoptados originalmente para cada una de las 28 secciones; cada una de estas cargas se obtiene sumando los pesos de los paneles situados sobre la sección considerada.

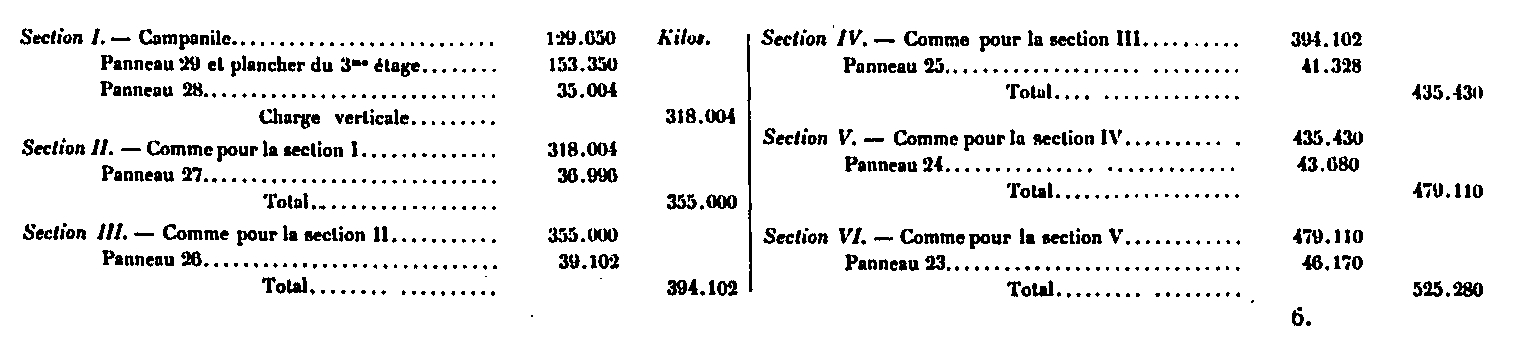
Cálculo de la parte superior

En la parte superior, sobre el segundo piso, las vigas son casi verticales y la influencia de su inclinación es insensible. Obtenemos directamente el coeficiente de trabajo R dividiendo el esfuerzo total P de las cargas situadas por encima de la sección considerada por la superficie total a de todos los ballesteros cortados, es decir que uno tiene R = ~. La siguiente tabla resume estos esfuerzos, que varían de 1K, 5 a 2K, 6, dejando así el margen necesario para la resistencia del viento, que juega un papel dominante en esta parte de la Torre.

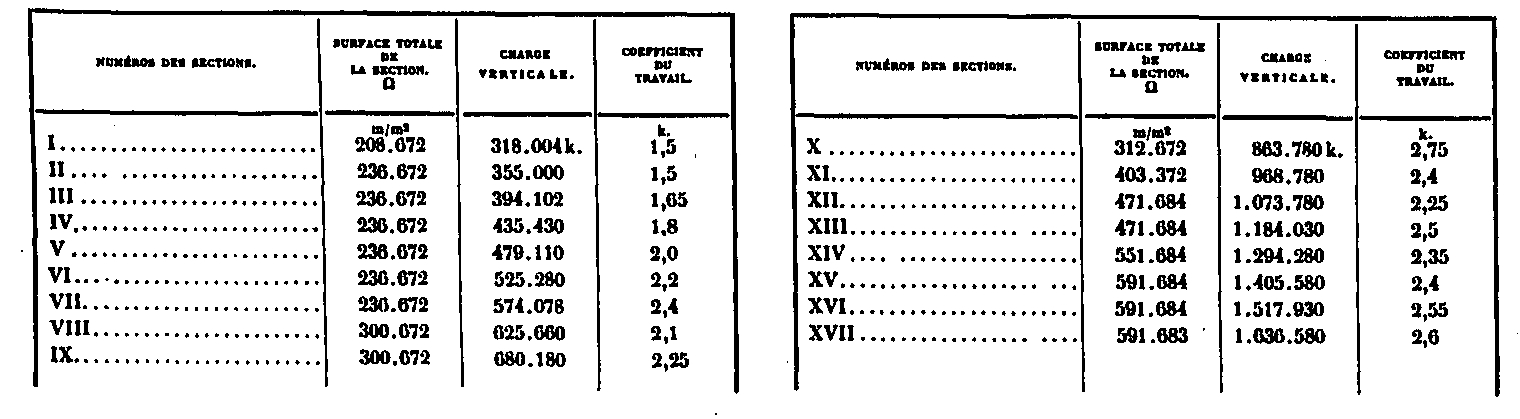
Cálculo de la parte inferior (Método utilizado)

Calcularemos para cada cantidad tomada de forma aislada. Los pesos totales de los diversos paneles de la Torre que hemos determinado por encima de P1, P2, ... se distribuyen por igual entre estas 4 cantidades: los pesos que usaremos en nuestros cálculos, son los pesos P1 = P1 / 4, P2 = P2 / 4, etc. Aplicados a los centros de figura de los paneles, centros cuyo ensamblaje constituye la fibra media. La fuerza fuera de una sección es el resultado de todas las cargas verticales y fuerzas horizontales que actúan sobre la sección. La componente vertical de esta fuerza es igual a las cargas; El componente horizontal resulta de la acción de las correas en la 1ª y 2ª plataforma. Primero, calcularemos como si el sistema estuviera articulado en los puntos α, β, reuniendo los puntos de las correas con la fibra promedio (Figura 1).

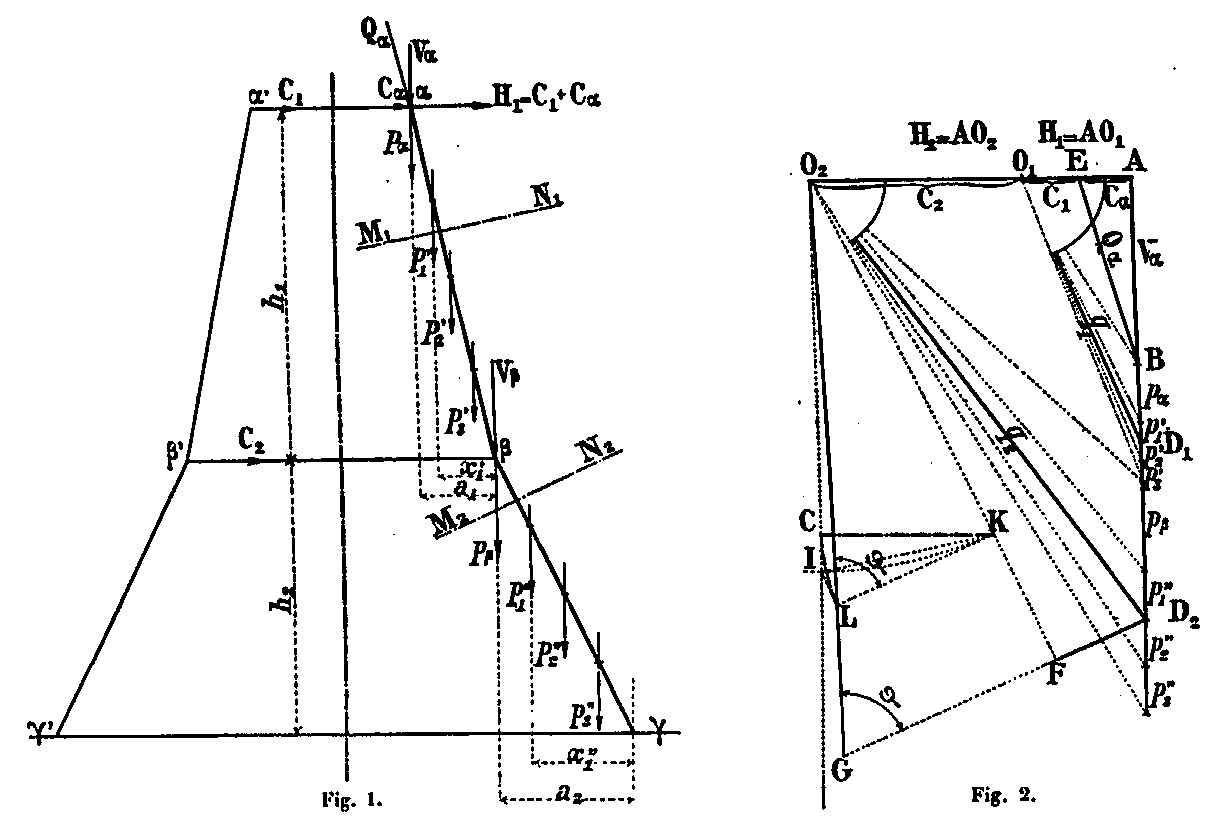
Sea Qα la resultante de las fuerzas que actúan sobre la cantidad por encima de la correa αα '; pasa, según la hipótesis aceptada, por el punto α de la fibra promedio y está en la dirección del elemento por encima de la correa.

• Sean Vα y Cα sus componentes verticales y horizontales.
• ρα = Pα / 4, el cuarto del peso total del piso del segundo piso ubicado en el cinturón αα '.
• C, la tensión en el cinturón αα '.
• a, el espaciado horizontal de los puntos αβ.
• x1 ', x2', x3 ', ... las distancias horizontales desde el punto β a los puntos de aplicación de carga ρ1', ρ2 ', ρ3' que actúan en la posición vertical entre las dos correas.
• h, la distancia de las correas α y β
• Finalmente, H1, la resultante de las fuerzas horizontales que actúan en el punto α y cuyo valor es H1 = Cα + C1. Para tener el valor de H1, basta, ya que la cantidad αβ está en equilibrio, para igualar el momento de las fuerzas verticales externas con respecto al punto β, a la de la resultante horizontal tomada con respecto a este mismo punto, que da H1ρ1 = (Vα + ρα) a1 + ρ1'x1 '+ ρ2'x2' + ... de donde derivamos H1 = 1 / ρ1 [(Vα + ρα) a1 + ρ1'x1 '+ ρ2'x2' + ...], una expresión en la que todos los elementos son conocidos.

Uno tendría lo mismo para la parte βΥ = 1 / ρ2 [(Vβρβ) a2 + ρ1'x1 '+ ρ2'x2' + ...] en la que Vβ representa la suma de todas las fuerzas verticales que actúan sobre la correa ββ.

• ρβ un cuarto del peso del piso del primer piso ubicado en el cinturón ββ '.
• ρ1 ", ρ2", etc. las cargas en la cantidad por debajo del cinturón β β '.
• x1 ', x2', x3 ', ... su influencia con respecto al punto Υ
• a2 el espaciado horizontal de los puntos β y Υ.
• ρ2 el espaciado de las correas β y Υ

Conociendo H1 y H2, uno puede construir los polígonos de las fuerzas, uno de los cuales, de distancia polar AO1 = H1 se aplicará a la parte αβ, el otro, de distancia polar AO2 = H2, a la parte βΥ (fig. 2).

Para cualquier sección M1N1 entre las correas αα '; y ββ ', la fuerza externa viene dada por el radio O2D2, que comienza desde el polo O2, y pasa a través del punto D1 de separación de las fuerzas ρ1 y ρ2 entre las cuales se encuentra la sección M1N1.

Para una sección M2N2, hecha debajo de la correa ββ ', la fuerza externa viene dada por el radio O2D2 que comienza desde el polo O2 y termina en el punto D2, situado entre las fuerzas ρ1 "y ρ2".

La distancia de los polos O1 y O2 es igual a la fuerza de compresión C2 de la correa ββ 'que tiene el valor H2 - H1.

En cuanto a las fuerzas Cα y 1, la primera está determinada por el extremo B de la línea AB = Vα, un paralelo al elemento sobre la correa: AE es esta fuerza. Como resultado, O1E es la fuerza C1 y EB = Qα.

Al tener fuerzas externas, como q1q2, se obtendrán las fuerzas de compresión y las fuerzas de cizallamiento al descomponer cada una de ellas en dos fuerzas: una paralela a la fibra promedio en la sección considerada y la otra normal en esta dirección. La fuerza de compresión así obtenida es la que actúa en el plano vertical, debe devolverse al plano de la cantidad y descomponerse de acuerdo con la inclinación de la cantidad en el plegado.

Esta descomposición se indica en la figura para la fuerza externa q2 = O2D2 de la sección M2N2; En primer lugar, dibujando la línea O2F paralela a la fibra promedio y bajando la D2F perpendicular, una fuerza de corte D2F y una fuerza de compresión O2F que actúan en el plano vertical. Para devolverlo al plano de la cara, el plegado se realiza de la siguiente manera (Fig. 3):

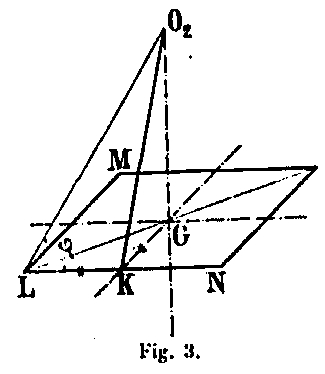
Desde el polo O2 como centro, trazamos un arco desde el punto I ubicado en la vertical del polo en el punto K en O2F. Desde el punto K elevamos una KL perpendicular a O2F y desde el punto I una IL perpendicular a KL. El punto L es la intersección de estas dos líneas. O2L es la dirección deseada de la fuerza de acuerdo con el plan de monto. De hecho: MN es un plano horizontal, para que O2L conozca O2K, es suficiente tener la longitud KL = KC y llevarlo en una perpendicular a O2K elevado al punto K. Para tener KC es necesario bajar desde el punto K a perpendicular En la vertical O2C. Al reducir la longitud obtenida en la dirección KL, tenemos el punto L buscado que también se puede obtener por la construcción indicada en el boceto (Fig. 2), porque en el triángulo ILK se obtiene liderando las perpendiculares KL y IL, tenemos KL = KC. Al proyectar la fuerza de O2F normalmente en su dirección en la dirección de O2L, finalmente obtenemos la fuerza de O2G que es la fuerza de compresión real de la cantidad. Esta fuerza N da, en cada uno de los 4 ballesteros, a, b, c, d de la cantidad, una fuerza E, = N2 / 4.

En cuanto a la fuerza de corte F2, se llevará en una línea normal a la fibra promedio y se descompone en la dirección de las barras de celosía correspondientes, lo que dará el esfuerzo en cada una de ellas para todas las dos caras. En realidad, el sistema que estudiamos no está articulado, sino que está incrustado en la base así como en los puntos α, β como resultado de la continuidad de la cantidad, y tomaremos en cuenta esta continuidad en la Cálculo de los momentos de flexión debidos a la inclinación de los montantes y a la acción de las cargas verticales que actúan contra los puntos de apoyo formados por las correas.

Primero notaremos que la primera hipótesis que se ha utilizado para determinar las fuerzas no cambia de ninguna manera el valor absoluto de las fuerzas de compresión y las fuerzas de corte reales: corresponde solo a un desplazamiento de la curva de las presiones reales paralelas a él. -incluso. La curva de las presiones reales se puede trazar con el mismo polígono de fuerzas que la fig. 2.

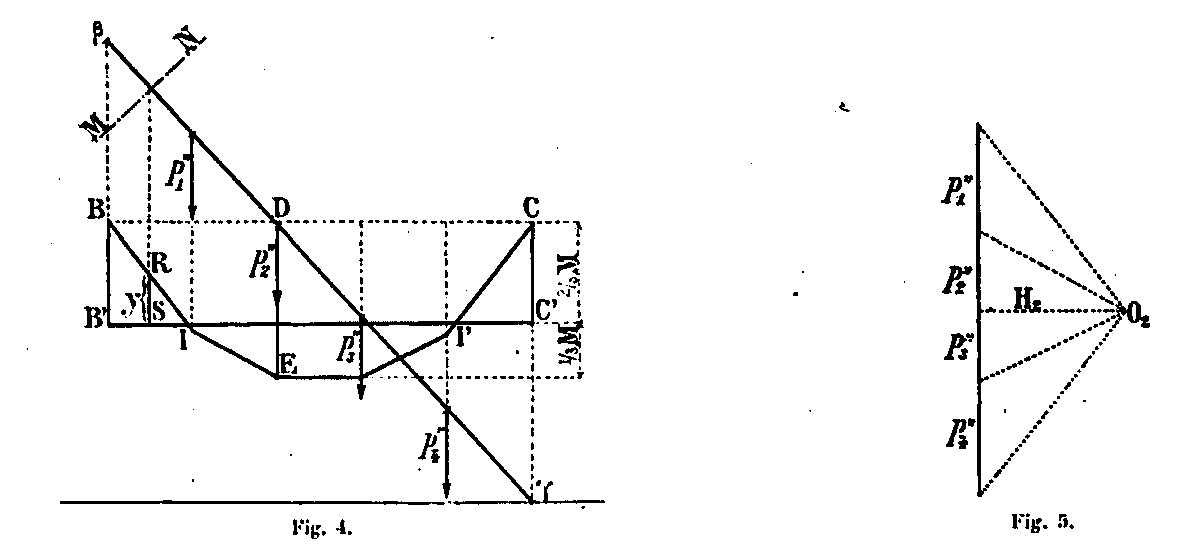
En considérant la partie βϒ, on peut tracer le polygone funiculaire BEC (fig. 4) correspondant au polygone des forces ρ1' ρ2'ρ3'ρ4' qui agissent sur la partie βϒ. On sait d'autre part que si M est le moment maximum d'une poutre uniformément chargée et reposant librement sur ses appuis, les moments de la même poutre encastrée à chacune de ses extrémités sont de :

2/3 M sur les appuis et 1/3 M au milieu de la travée. D'après notre hypothèse d'encastrement, nous avons donc en β et ϒ des moments d'encastrement BB' — CC' égaux aux 2/3 du moment maximum DE, qui se produirait si le montant était articulé en β et ϒ. Les moments sont représentés en un point quelconque par les ordonnées du polygone funiculaire mesurées à partir de la ligne B'C parallèle à BC et distante verticalement de celle-ci des 2/3 du moment DE. Ils sont positifs dans les parties B'I et I'C' et sont négatifs entre les points I et I'. Pour une section MN, le moment est égal à μ = RS x H2 ϒH2.

On calculera de la même manière les moments fléchissants dus au poids propre dans la partie αβ du montant comprise entre la deuxième et la première plate-forme. Le moment ainsi déterminé agit dans le plan vertical XY. Il est produit par l'inclinaison α1 de la projection du montant sur ce plan. On a de même dans le plan vertical UZ, perpendiculaire à XY, un moment qui est dû à l'inclinaison du montant suivant la direction UZ. Les inclinaisons α1, étant les mêmes dans les deux sens XY et UZ, ces deux moments sont égaux. Pour obtenir les couples correspondants qui agissent dans les faces du montant, il faut décomposer ces deux couples μ suivant l'inclinaison des faces. Soient RS, l'axe représentatif du moment μ1 dans le plan XY, R'S', l'axe représentatif de ce même moment dans le plan UZ. Pour les composer entre eux, nous décomposerons chacun d'eux suivant la verticale et suivant une normale à la libre moyenne, ST et RT = μ1 / sin α, S'T' et R'T' = μ1 / sin α. Les composantes verticales ST, S'T', étant égales et de signe contraire s'annulent; les composantes normales RT, R'T' subsistent seules.

Le moment RT produit dans les parois ab et dc, pour des valeurs positives du moment, un effort de compression sur les arbalétriers a et d et une tension dans les arbalétriers b et c. De même le moment R'T', dans le plan vertical UZ, produit dans les parois ad et bc un effort de compression pour les arbalétriers a et b et une tension pour les arbalétriers d et c.

En désignant par E', l'effort dans les arbalétriers, et i, leur écartement, μ1 / sin α1 étant le moment relatif à l'ensemble des deux faces ab et dc, on a pour l'une d'elles E'i = (I/2) x (μ1 / sin α1) d'où E' = (I/2i) x (μ1 / sin α1). Cet effort E' donne une compression sur les arbalétriers a et d et une tension sur les arbalétriers b et c. On aurait de même pour les faces ad et bc, l'effort E" = (I/2i) x (μ1 / sin α1) qui donne une compression sur les arbalétriers a et b et une tension sur les arbalétriers d et c.

Les efforts totaux de compression seront donc : pour l'arbalétrier a E2 = μ1 / (i sin α1) et les efforts totaux de tension : pour l'arbalétrier c E2 = μ1 / (i sin α1). Pour les arbalétriers b et d, les efforts s'annulent. Les efforts totaux produits dans les arbalétriers de la partie inférieure par l'effet des charges verticales, en tenant compte des moments fléchissants est ainsi

• pour l'arbalétrier a un effort de Ea = E1 + E2
• pour l'arbalétrier c un effort de Ec = E1 - E2
• pour l'arbalétrier b ou d un effort de Eb, d = E1

Sección inferior (cálculos numéricos)

Primero debemos determinar los valores de H ₁ y H₂, es decir, las fuerzas horizontales que actúan a la derecha de las correas. Las tablas de abajo dan los cálculos.

Cálculo del empuje horizontal H, debido a las cargas verticales entre las correas de primera y segunda etapa

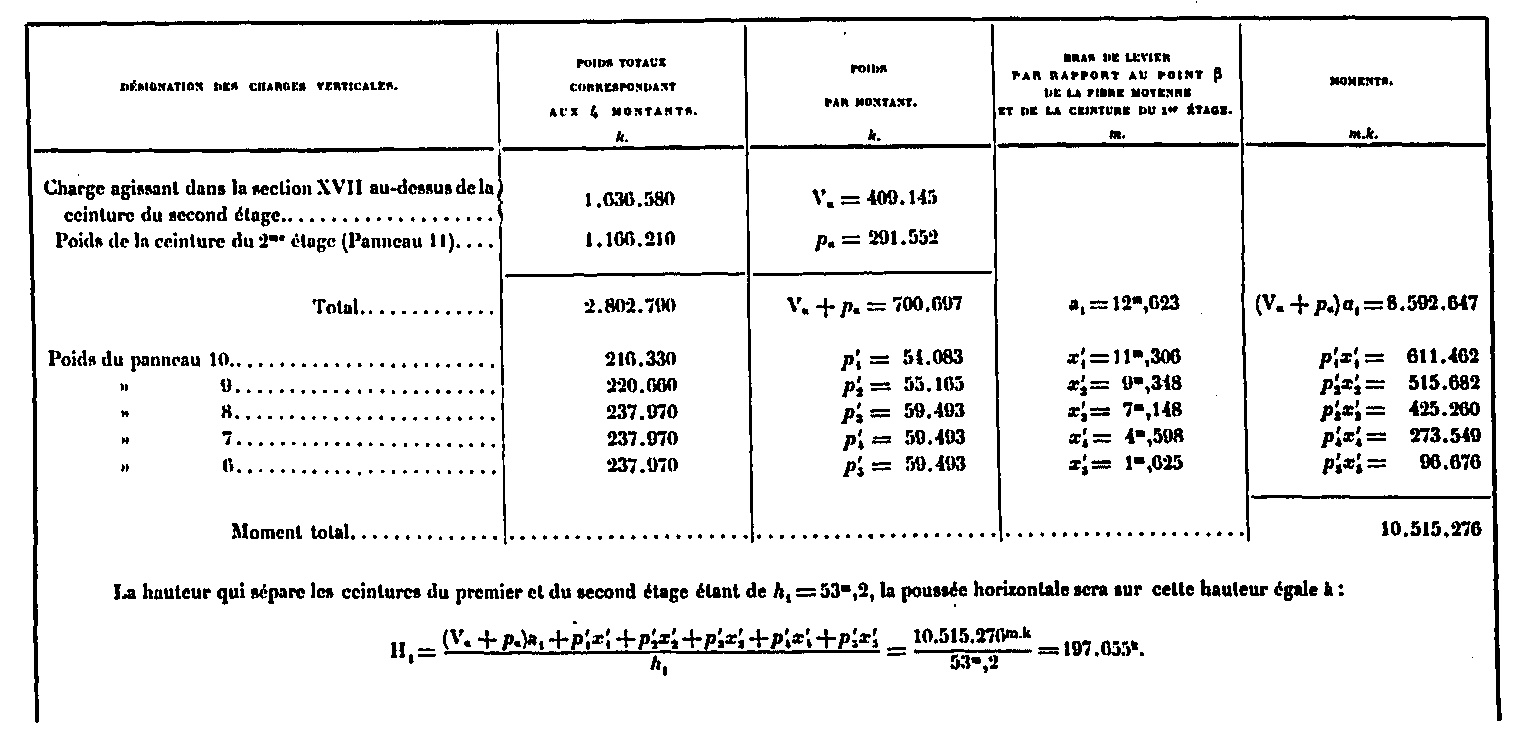
Cálculo del empuje horizontal H2 debido a las cargas verticales debajo de la primera etapa ββ 'cinturón

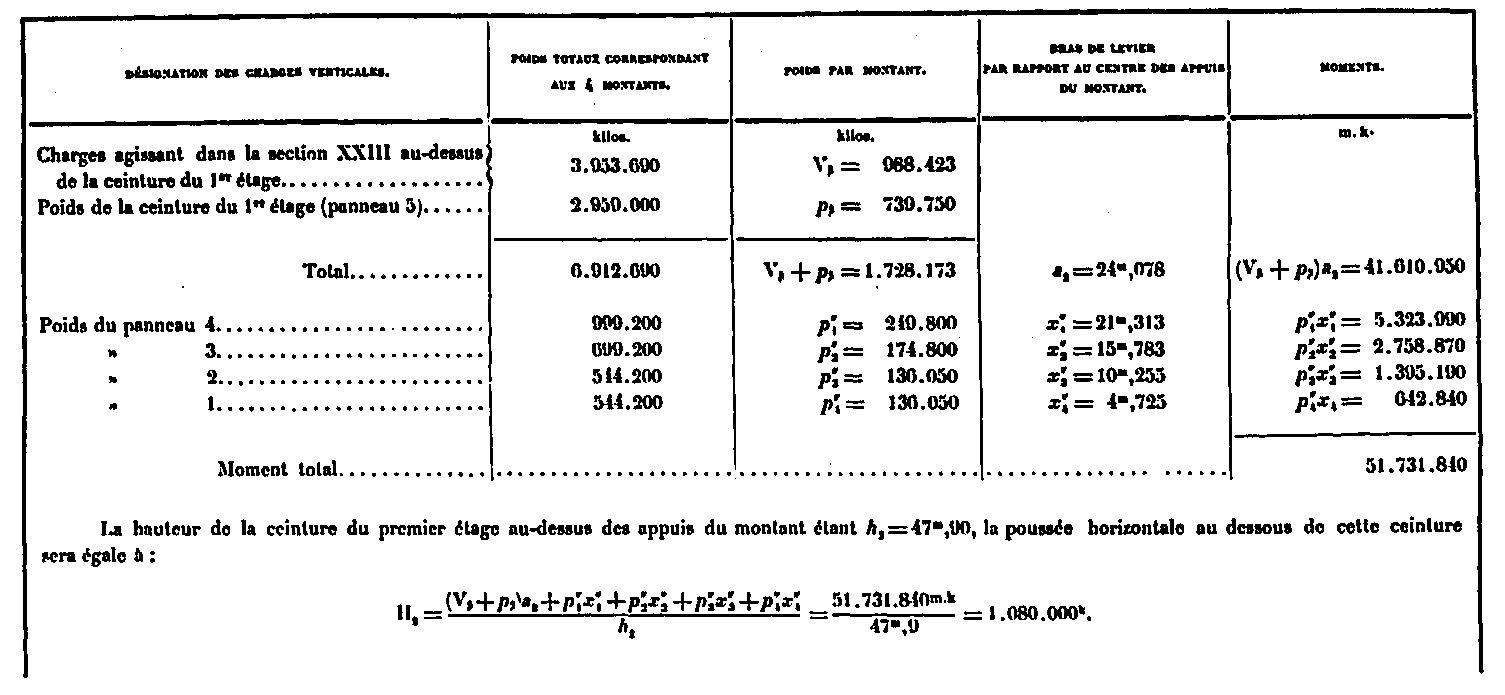
Estos valores que se encuentran en cada una de las cantidades, en la segunda plataforma: 197 655Kg, en la primera plataforma 1 080 000Kg, permiten establecer los polígonos de fuerza de la figura 6 de la placa XXXII, de acuerdo con el método dado arriba, para la Figura 2. Deducimos todos los valores de N2, fuerza de compresión de la cantidad y, por lo tanto, E1 = fuerza de compresión de N / 4 de cada uno de los ballesteros. También dibuja el valor de las fuerzas de corte como D2F de la misma figura. Estos valores se enumeran en la siguiente tabla:

En cuanto a los esfuerzos en los ballesteros debido a los momentos de flexión, vimos que estaban representados por la expresión E2 = μ / (i sin α1) en la que:

• i es el espaciamiento normal de los ballesteros
• α1 el ángulo de inclinación en la horizontal de la proyección de la fibra promedio en el plano vertical
• μ1, las ordenadas con respecto a B'C (ver Fig. 4) polígonos funiculares construidos con polígonos de fuerzas verticales entre α y β y entre β y Υ.

Estos polígonos se muestran en las Figuras 4 y 8 de la Placa XXXII. La distancia polar fue tomada desde 100,000K. La escala de longitudes es 0m, 003 por metro, la escala de los momentos será 0m, 003 por 100 000 m. K.

Llegamos así a la siguiente tabla:

Las fuerzas totales en cada uno de los ballesteros, así como los coeficientes de trabajo, se dan en la siguiente tabla:

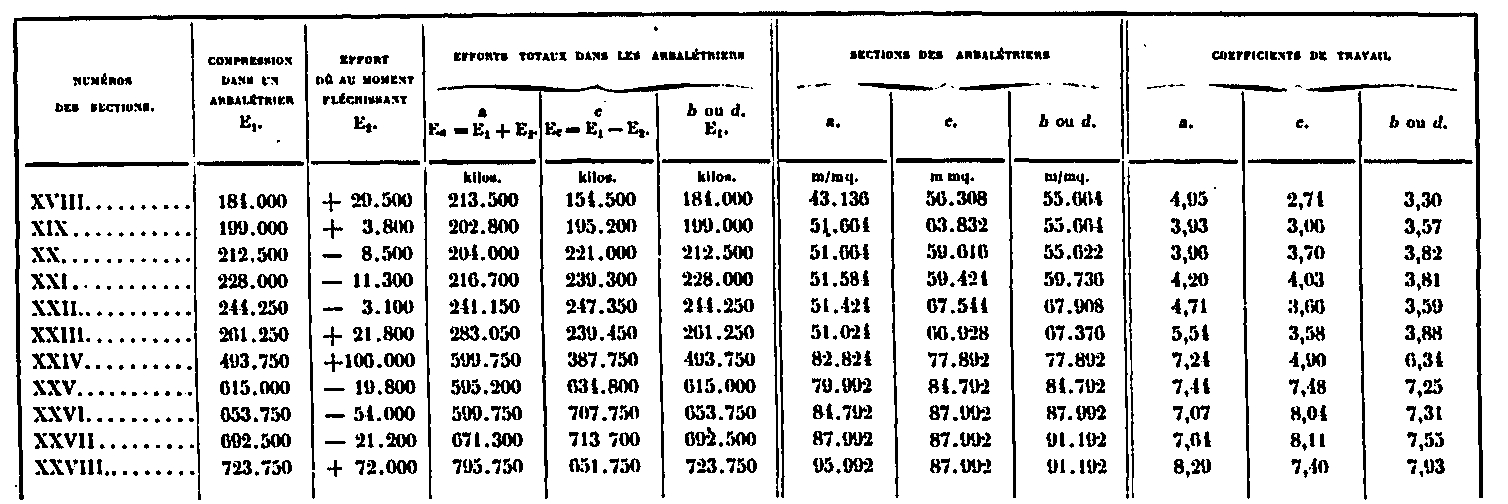
En cuanto a las barras de celosía, sus coeficientes de trabajo están dados por la siguiente tabla:

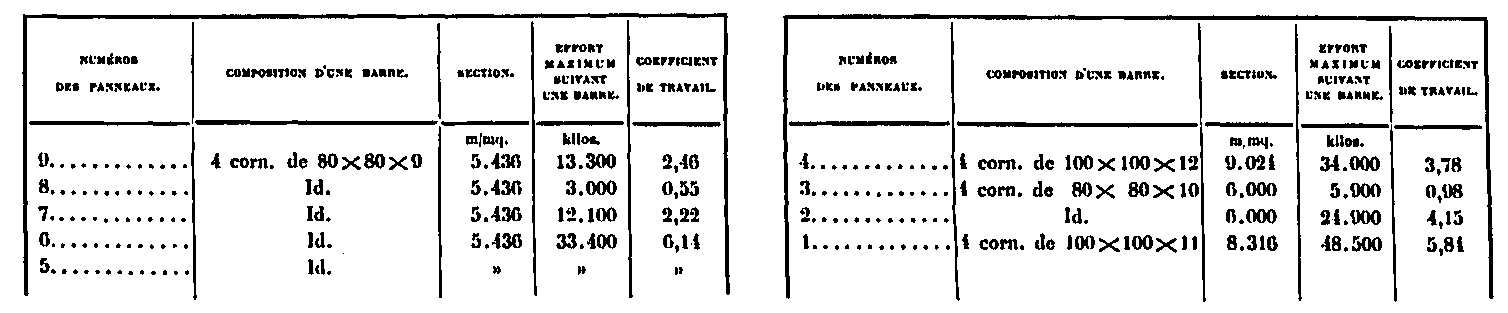
Estos son los efectos del peso de la construcción de la Torre Eiffel. Tienes los cálculos de la estructura para la resistencia al viento en esta página.